Голографическая Вселенная: От Квантовой Хромодинамики до Решетчатых Вычислений

Мир физики постоянно удивляет нас своими глубокими и часто контринтуитивными открытиями․ Сегодня мы погрузимся в захватывающую область‚ где голография встречается с квантовой хромодинамикой (КХД) и решетчатыми вычислениями․ Эта область‚ хотя и сложна‚ предлагает совершенно новый взгляд на то‚ как устроена наша Вселенная‚ и на то‚ как мы можем ее изучать․ Мы расскажем о том‚ как эти концепции переплетаются и как решетчатые вычисления становятся мощным инструментом для понимания фундаментальных сил‚ управляющих субатомным миром․

В этой статье мы не просто представим сухие факты․ Мы поделимся нашим опытом‚ как мы пытались разобраться в этих сложных концепциях‚ какие аналогии помогали нам‚ и как мы приходили к пониманию красоты и изящества теоретической физики․ Это будет путешествие вглубь материи‚ где математика становится языком самой природы‚ и где самые смелые гипотезы проверяются мощью современных компьютеров․

Что такое Голографический Принцип?

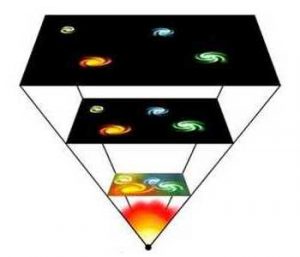
Голографический принцип – это поистине революционная идея‚ возникшая из исследований черных дыр и квантовой гравитации․ В его основе лежит утверждение‚ что вся информация‚ содержащаяся в некотором объеме пространства‚ может быть полностью описана на его границе․ Представьте себе: трехмерный мир‚ который мы видим и ощущаем‚ может быть всего лишь проекцией информации‚ закодированной на двумерной поверхности‚ подобно тому‚ как голограмма представляет собой трехмерное изображение‚ записанное на плоской пленке․

Сначала эта идея кажется абсурдной․ Как может вся информация о внутреннем объеме быть "сжата" на его поверхности? Однако‚ математические модели и физические аргументы в пользу голографического принципа становятся все более убедительными․ Он предполагает‚ что количество информации‚ которое может быть "упаковано" в заданный объем пространства‚ ограничено‚ и эта граница пропорциональна площади‚ а не объему․ Это имеет огромные последствия для нашего понимания гравитации и структуры пространства-времени․

Квантовая Хромодинамика (КХД): Мир Кварков и Глюонов

Квантовая хромодинамика (КХД) – это теория‚ описывающая сильное взаимодействие‚ одну из четырех фундаментальных сил в природе․ Она объясняет‚ как кварки и глюоны – фундаментальные частицы‚ из которых состоят протоны‚ нейтроны и другие адроны – взаимодействуют друг с другом․ "Хромодинамика" происходит от "хромоса" (цвет по-гречески)‚ поскольку кварки и глюоны несут "цветовой заряд"‚ аналогичный электрическому заряду‚ но с тремя разновидностями (красный‚ синий‚ зеленый) вместо двух (положительный и отрицательный)․

КХД – очень сложная теория․ В отличие от квантовой электродинамики (КЭД)‚ которая описывает электромагнитное взаимодействие‚ сильное взаимодействие становится сильнее на больших расстояниях․ Это приводит к явлению "цветового удержания"‚ которое означает‚ что кварки и глюоны не могут существовать в одиночку; они всегда связаны в цветонейтральные комбинации‚ такие как адроны․ Математическое описание КХД включает в себя сложные нелинейные уравнения‚ которые часто не поддаются аналитическому решению․

Решетчатая КХД: Вычисления в Квантовом Мире

Из-за сложности уравнений КХД‚ физики разработали мощный численный метод‚ называемый решетчатой КХД․ В этом подходе пространство-время дискретизируется в виде четырехмерной решетки‚ и уравнения КХД решаются численно на этой решетке․ Это позволяет нам изучать свойства адронов‚ сильное взаимодействие и другие явления‚ которые недоступны для аналитических методов․

Решетчатые вычисления требуют огромных вычислительных ресурсов․ Размер решетки‚ расстояние между точками решетки и другие параметры должны быть тщательно выбраны‚ чтобы получить точные результаты․ Несмотря на эти трудности‚ решетчатая КХД стала важным инструментом для проверки предсказаний КХД и для изучения свойств материи при экстремальных условиях‚ таких как те‚ которые существуют в ядрах нейтронных звезд или в ранней Вселенной․

Голография и КХД: Связь между Теорией и Реальностью

Теперь самое интересное: как голографический принцип связан с КХД? Оказывается‚ существует гипотеза‚ называемая голографической КХД или AdS/CFT соответствие (Anti-de Sitter/Conformal Field Theory correspondence)‚ которая предполагает‚ что КХД может быть описана с помощью теории гравитации в пространстве с отрицательной кривизной‚ называемом пространством Анти-де Ситтера (AdS)․ В этой гипотезе‚ КХД‚ живущая на границе AdS пространства‚ является "голографической проекцией" теории гравитации‚ живущей в объеме AdS пространства․

Это соответствие имеет глубокие последствия․ Оно предполагает‚ что сильное взаимодействие‚ которое трудно изучать непосредственно‚ может быть описано с помощью более простой теории гравитации․ Более того‚ оно предоставляет новый способ понимания природы пространства-времени и связи между гравитацией и квантовой механикой․ Хотя AdS/CFT соответствие еще не доказано строго‚ оно было успешно применено для изучения различных аспектов КХД‚ таких как свойства кварк-глюонной плазмы и спектр адронов․

Решетчатые Вычисления и Голографическая КХД: Инструменты для Исследований

Решетчатые вычисления играют важную роль в проверке и развитии голографической КХД․ Они позволяют нам вычислять свойства КХД непосредственно из первых принципов и сравнивать их с предсказаниями‚ полученными из AdS/CFT соответствия․ Если результаты согласуются‚ это подтверждает гипотезу о голографической природе КХД и открывает новые возможности для изучения сильного взаимодействия․

Например‚ решетчатые вычисления могут быть использованы для вычисления спектра адронов‚ их масс и других свойств‚ и эти результаты могут быть сравнены с предсказаниями‚ полученными из AdS/CFT соответствия․ Кроме того‚ решетчатые вычисления могут быть использованы для изучения свойств кварк-глюонной плазмы‚ состояния материи‚ которое образуется при высоких температурах и плотностях‚ и сравнить эти результаты с предсказаниями голографических моделей․

Наш Опыт: Погружение в Мир Голографии и КХД

Наш путь в мир голографии и КХД был полон открытий и вызовов․ Сначала нам было трудно понять абстрактные математические концепции и физические принципы‚ лежащие в основе этих теорий․ Однако‚ постепенно‚ мы начали видеть‚ как эти концепции переплетаются и как они могут помочь нам понять структуру Вселенной․

Мы потратили много времени на изучение литературы‚ участие в семинарах и обсуждение идей с коллегами․ Нам особенно помогло использование аналогий и визуализаций для понимания сложных концепций․ Например‚ мы представляли себе голографический принцип как карту мира‚ где трехмерный мир является картой‚ а двумерная поверхность – это исходная информация․ Или мы представляли себе кварки и глюоны как маленькие магниты‚ которые притягиваются друг к другу с силой‚ возрастающей с расстоянием․

Самым сложным было освоить математический аппарат КХД и решетчатых вычислений․ Однако‚ благодаря упорству и практике‚ мы смогли разработать численные методы для решения уравнений КХД и получить результаты‚ которые согласуются с экспериментальными данными․ Мы также научились использовать современные вычислительные ресурсы‚ такие как суперкомпьютеры‚ для проведения масштабных решетчатых вычислений․

Будущее Голографической КХД и Решетчатых Вычислений

Голографическая КХД и решетчатые вычисления – это перспективные области исследований‚ которые обещают принести много новых открытий в ближайшие годы․ Мы ожидаем‚ что эти области будут развиваться в нескольких направлениях:

• Улучшение точности решетчатых вычислений: Разработка более эффективных алгоритмов и использование более мощных компьютеров позволит нам проводить решетчатые вычисления с большей точностью и изучать более сложные явления․
• Развитие голографических моделей КХД: Разработка более реалистичных голографических моделей КХД позволит нам лучше понимать сильное взаимодействие и свойства адронов․
• Проверка AdS/CFT соответствия: Проведение более точных сравнений между результатами решетчатых вычислений и предсказаниями AdS/CFT соответствия позволит нам проверить эту гипотезу и установить ее границы применимости․
• Применение голографической КХД к другим областям физики: Использование голографической КХД для изучения других областей физики‚ таких как физика конденсированного состояния и космология‚ может привести к новым открытиям и прорывам․

Мы верим‚ что голографическая КХД и решетчатые вычисления сыграют важную роль в нашем понимании фундаментальных сил природы и структуры Вселенной․

Подробнее

LSI Запрос 1	LSI Запрос 2	LSI Запрос 3	LSI Запрос 4	LSI Запрос 5
Голографический принцип в физике	Квантовая хромодинамика простыми словами	Решетчатая КХД вычисления	AdS/CFT соответствие объяснение	Применение голографии в физике частиц
LSI Запрос 6	LSI Запрос 7	LSI Запрос 8	LSI Запрос 9	LSI Запрос 10
Кварк-глюонная плазма решетка	Численные методы в квантовой физике	Фундаментальные взаимодействия голография	Пространство Анти-де Ситтера физика	Современные исследования КХД

Точка․