Математический аппарат теории струн: Путешествие в неизведанное

Приветствую вас, дорогие читатели! Сегодня мы отправимся в захватывающее путешествие в мир теории струн – одну из самых амбициозных и сложных областей современной физики. Мы не будем углубляться в дебри сложных уравнений, но постараемся понять, как математика становится языком, на котором Вселенная раскрывает свои самые сокровенные тайны. Вместо того, чтобы говорить "я", мы будем говорить "мы", ведь это общее приключение, которое мы совершим вместе.

Теория струн – это попытка объединить общую теорию относительности Эйнштейна, описывающую гравитацию и крупномасштабную структуру Вселенной, с квантовой механикой, описывающей мир элементарных частиц. Эта задача оказалась невероятно сложной, поскольку обе теории работают прекрасно в своих областях, но при попытке объединения возникают серьезные противоречия. Теория струн предлагает радикально новый взгляд на фундаментальные строительные блоки материи.

Что такое теория струн?

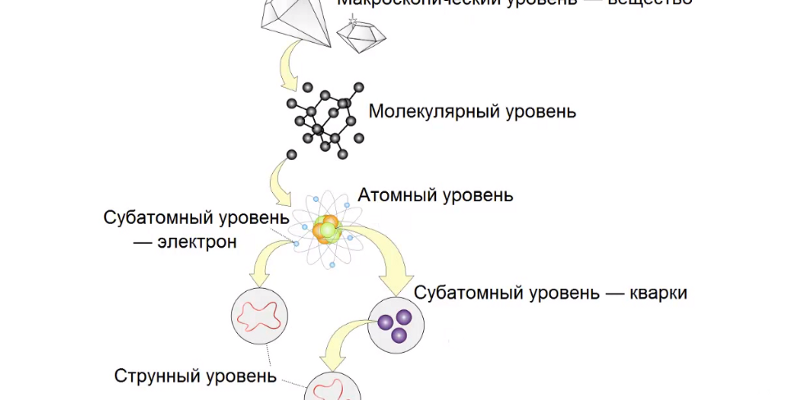
Вместо того чтобы рассматривать элементарные частицы как точечные объекты, теория струн предполагает, что они являются крошечными вибрирующими струнами. Различные моды вибрации этих струн соответствуют различным частицам – электронам, кваркам, нейтрино и т.д.. Представьте себе скрипку: разные ноты возникают из-за разных способов вибрации струны. Аналогично, разные частицы возникают из-за разных способов вибрации фундаментальных струн.

Эта идея имеет далеко идущие последствия. Во-первых, она автоматически включает в себя гравитацию, что является огромным достижением. Во-вторых, она требует существования дополнительных измерений пространства-времени. Вместо привычных нам трех пространственных измерений и одного временного, теория струн предсказывает наличие, как минимум, десяти измерений. Эти дополнительные измерения свернуты в крошечные, невидимые структуры, известные как многообразия Калаби-Яу.

Математика как язык Вселенной

Математический аппарат теории струн чрезвычайно сложен и требует глубоких знаний в различных областях математики, таких как:

• Дифференциальная геометрия: для описания многообразий Калаби-Яу и других геометрических объектов.
• Топология: для изучения свойств пространства, которые не меняются при непрерывных деформациях.
• Алгебра: для работы с группами симметрий и алгебрами Ли;
• Комплексный анализ: для описания струнных амплитуд и других физических величин.

Нам часто кажется, что математика – это что-то абстрактное и оторванное от реальности. Но в теории струн математика становится не просто инструментом, а самим языком, на котором Вселенная говорит с нами. Уравнения – это не просто символы на бумаге, а отражение глубоких и фундаментальных законов природы.

Геометрия и топология в теории струн

Геометрия и топология играют центральную роль в теории струн. Многообразия Калаби-Яу, в которых свернуты дополнительные измерения, являются сложными геометрическими объектами, требующими глубокого математического анализа. Топология позволяет нам изучать свойства этих многообразий, которые не меняются при деформациях, например, количество "дыр" в них. Эти топологические свойства, в свою очередь, определяют физические характеристики Вселенной, такие как количество поколений элементарных частиц.

Представьте себе, что мы живем на поверхности пончика. С точки зрения геометрии, это кривая поверхность с определенной кривизной. Но с точки зрения топологии, пончик отличается от сферы (например, футбольного мяча) тем, что у него есть одна "дыра". Именно эта "дыра" делает пончик пончиком. Аналогично, топологические свойства многообразий Калаби-Яу определяют фундаментальные свойства нашей Вселенной.

Алгебра и симметрии

Симметрии играют ключевую роль в физике. Они позволяют нам выявлять законы сохранения и упрощать сложные задачи. В теории струн симметрии приобретают еще большее значение. Они не только описывают известные нам законы природы, но и предсказывают новые, еще не открытые.

Алгебра Ли – это математический аппарат, используемый для описания непрерывных симметрий. В теории струн используются сложные алгебры Ли, такие как алгебра Вирасоро, которая описывает конформную симметрию. Эти алгебры позволяют нам вычислять струнные амплитуды – вероятности различных процессов, происходящих с участием струн.

Вычислительные трудности и перспективы

Несмотря на всю красоту и элегантность теории струн, она сталкивается с серьезными вычислительными трудностями. Уравнения, описывающие динамику струн, чрезвычайно сложны и не имеют аналитических решений. Это означает, что мы не можем просто взять и решить эти уравнения, чтобы получить конкретные предсказания.

Для решения этих проблем используются различные методы приближенного вычисления, такие как теория возмущений и численные методы. Теория возмущений позволяет нам вычислять струнные амплитуды в виде бесконечных рядов. Численные методы позволяют нам моделировать динамику струн на компьютерах. Однако, оба этих метода имеют свои ограничения.

Несмотря на эти трудности, теория струн продолжает развиваться. Новые идеи и методы появляются постоянно. Возможно, в будущем нам удастся преодолеть все вычислительные трудности и получить конкретные предсказания, которые можно будет проверить экспериментально.

Будущее теории струн

Теория струн – это не просто физическая теория, а целая программа исследований, направленная на понимание фундаментальных законов природы. Она объединяет в себе физику, математику, космологию и даже философию. Несмотря на то, что у нас пока нет прямых экспериментальных подтверждений теории струн, она оказала огромное влияние на развитие теоретической физики.

Мы надеемся, что в будущем теория струн приведет к новым открытиям и технологиям. Возможно, она позволит нам создать новые материалы с уникальными свойствами, разработать новые источники энергии или даже построить космические корабли, способные перемещаться в другие измерения.

Экспериментальная проверка теории струн

Один из самых больших вызовов для теории струн – это отсутствие прямых экспериментальных подтверждений. Энергии, необходимые для проверки предсказаний теории струн, находятся за пределами возможностей современных ускорителей частиц. Однако, существуют косвенные способы проверки теории струн, например, через изучение космического микроволнового фона или поиск следов дополнительных измерений.

Некоторые физики считают, что теория струн никогда не будет экспериментально проверена и останется чисто математической теорией. Однако, мы верим, что в будущем появятся новые экспериментальные возможности, которые позволят нам проверить предсказания теории струн и подтвердить или опровергнуть ее справедливость.

Наше путешествие в мир математического аппарата теории струн подошло к концу. Мы увидели, как математика становится языком, на котором Вселенная раскрывает свои самые сокровенные тайны. Мы узнали о сложных геометрических объектах, алгебрах Ли и вычислительных трудностях, с которыми сталкиваются физики-теоретики. Мы надеемся, что это путешествие было для вас интересным и познавательным.

Теория струн – это не просто теория, а целое приключение, которое мы совершаем вместе; Это поиск истины, стремление к познанию и желание понять, как устроен наш мир. И мы верим, что в конце этого пути нас ждет открытие, которое изменит наше представление о Вселенной.

Подробнее

Теория струн для начинающих	Математика струнной теории	Экспериментальная проверка струн	Дополнительные измерения	Многообразия Калаби-Яу
Квантовая гравитация струны	История теории струн	Струны и космология	Алгебра Ли в физике	Вибрации струн