Струнные Компактные Пространства: Путешествие в Бесконечность

Мы‚ как исследователи математических глубин‚ часто сталкиваемся с концепциями‚ которые на первый взгляд кажутся абстрактными и далекими от реальности. Однако‚ именно в этих абстракциях кроются ключи к пониманию фундаментальных законов мироздания. Одной из таких концепций является понятие "струнного компактного пространства" в топологии. Это не просто набор символов и формул – это целый мир‚ полный изящества и гармонии‚ который мы сейчас попробуем исследовать.

Представьте себе Вселенную‚ не как трехмерное пространство‚ к которому мы привыкли‚ а как многомерное полотно‚ где каждый узел и каждая нить связаны между собой невидимыми связями. Именно эти связи‚ эти отношения между точками и множествами‚ и изучает топология. А струнные компактные пространства – это особый вид таких многомерных полотен‚ обладающих уникальными свойствами.

Что такое Топология и Компактность?

Прежде чем углубиться в струнные компактные пространства‚ нам необходимо понять два ключевых понятия: топологию и компактность. Топология‚ в самом широком смысле‚ – это изучение свойств‚ которые остаются неизменными при непрерывных деформациях. Представьте себе‚ что у вас есть кусок глины. Вы можете мять его‚ растягивать‚ скручивать‚ но при этом не разрывать и не склеивать его. Топология интересуется тем‚ что остается неизменным в процессе этих деформаций. Например‚ количество дырок в глине – это топологический инвариант.

Компактность‚ с другой стороны‚ – это свойство пространства‚ которое‚ грубо говоря‚ означает‚ что из любого бесконечного набора точек в этом пространстве можно выбрать подпоследовательность‚ которая сходится к точке‚ принадлежащей этому же пространству. Более формально‚ компактное пространство ー это пространство‚ из каждого открытого покрытия которого можно выделить конечное подпокрытие. Это определение может показатся сложным‚ но его суть заключается в том‚ что компактные пространства "хорошо себя ведут" в отношении бесконечных процессов.

Струнные Пространства: Добавляем Изящество

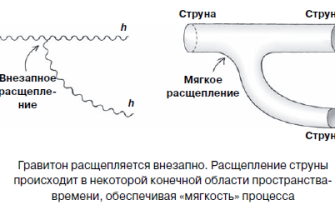
Теперь давайте поговорим о "струнных" пространствах. Этот термин‚ как правило‚ используется в контексте теоретической физики‚ а именно в теории струн. Теория струн предполагает‚ что элементарные частицы – это не точечные объекты‚ а крошечные вибрирующие струны. Пространство‚ в котором эти струны существуют и взаимодействуют‚ должно обладать определенными свойствами‚ чтобы теория была математически согласованной и соответствовала наблюдаемым явлениям.

Одним из важных требований является компактность дополнительных измерений. В теории струн обычно рассматриваются пространства с 10 или 11 измерениями. Поскольку мы наблюдаем только 3 пространственных и 1 временное измерение‚ остальные измерения должны быть "свернуты" в очень маленькие компактные пространства‚ которые мы не можем непосредственно наблюдать. Эти компактные пространства часто называют пространствами Калаби-Яу или орбифолдами.

Почему Компактность Важна?

Компактность дополнительных измерений играет ключевую роль в теории струн по нескольким причинам:

• Конечность Физических Величин: Компактность обеспечивает конечность физических величин‚ таких как массы и заряды частиц. Без компактности в теории появляются расходимости‚ которые делают ее бессмысленной.
• Хиральность Фермионов: Компактные пространства с определенной геометрией могут объяснить хиральность фермионов‚ то есть различие между левыми и правыми частицами‚ которое наблюдается в природе.
• Размерность Пространства-Времени: Компактность позволяет объяснить‚ почему мы наблюдаем только 4 измерения пространства-времени. Остальные измерения "свернуты" и не проявляются на макроскопическом уровне.

Представьте себе длинный шланг; Если смотреть на него издалека‚ он кажется одномерной линией. Но если подойти ближе‚ то можно увидеть‚ что он имеет также круговое измерение. Точно так же и дополнительные измерения в теории струн "свернуты" в очень маленькие компактные пространства‚ которые мы не можем непосредственно наблюдать.

Примеры Струнных Компактных Пространств

Существует множество примеров струнных компактных пространств‚ которые изучаются в теории струн и математике. Вот некоторые из них:

1. Торы: Торы – это простые примеры компактных пространств‚ которые получаются путем склеивания противоположных сторон прямоугольника. Торы могут быть многомерными‚ и они часто используются в качестве модельных пространств для изучения свойств более сложных компактных пространств.
2. Пространства Калаби-Яу: Пространства Калаби-Яу – это сложные комплексные многообразия‚ обладающие специальными свойствами. Они играют важную роль в теории струн‚ поскольку они допускают существование суперсимметрии‚ которая является важным ингредиентом теории.
3. Орбифолды: Орбифолды – это пространства‚ которые получаются путем деления гладкого многообразия на группу дискретных преобразований. Орбифолды могут иметь особенности‚ но они все равно являются важными примерами струнных компактных пространств.

Каждое из этих пространств обладает уникальными свойствами‚ которые могут влиять на физические явления‚ которые наблюдаются в теории струн. Изучение этих пространств – это активная область исследований‚ которая требует глубоких знаний в математике и физике.

Сложности и Перспективы

Изучение струнных компактных пространств – это сложная задача‚ которая сталкивается с множеством трудностей. Во-первых‚ эти пространства часто являются очень сложными и трудноописуемыми. Во-вторых‚ для их изучения требуется глубокое знание математики‚ включая топологию‚ геометрию и алгебру. В-третьих‚ связь между математическими свойствами этих пространств и физическими явлениями‚ которые они описывают‚ часто является нетривиальной и требует дополнительных исследований.

Однако‚ несмотря на эти трудности‚ изучение струнных компактных пространств – это очень перспективное направление исследований. Оно может привести к лучшему пониманию фундаментальных законов природы‚ а также к разработке новых математических инструментов и методов. Мы верим‚ что в будущем мы сможем раскрыть все тайны этих загадочных пространств и использовать их для построения более полной и точной картины мира.

Будущее Исследований

В будущем мы планируем продолжить наши исследования в области струнных компактных пространств. Мы хотим разработать новые методы для изучения этих пространств‚ а также исследовать их связь с физическими явлениями‚ такими как темная материя и темная энергия. Мы также надеемся‚ что наши исследования помогут нам построить более полную и точную теорию квантовой гравитации‚ которая объединит общую теорию относительности Эйнштейна с квантовой механикой.

Это путешествие в бесконечность‚ в мир математических абстракций‚ которые‚ возможно‚ являются ключом к пониманию реальности. И мы рады‚ что можем разделить этот путь с вами.

Подробнее

Топология компактных пространств	Теория струн и геометрия	Пространства Калаби-Яу физика	Компактификация измерений	Математическая модель Вселенной
Орбифолды и особенности	Квантовая гравитация топология	Многообразия в теории струн	Струнные компактификации	Дополнительные измерения физика

Точка.