Струнные Компактные Пространства: Путешествие в Мир Топологии

Приветствую, дорогие читатели! Сегодня мы отправляемся в захватывающее путешествие по просторам топологии, чтобы исследовать удивительные и загадочные струнные компактные пространства․ Это может звучать как что-то из научно-фантастического романа, но поверьте, это вполне реальная и очень интересная область математики․ Вместе мы попытаемся разобраться в сложных концепциях простым и доступным языком, основываясь на нашем личном опыте изучения этой темы․

Мы помним, как впервые столкнулись с понятием "струнного компактного пространства"․ Это было похоже на погружение в глубокий океан, где каждый новый термин и теорема казались неизведанными островами․ Однако, шаг за шагом, мы начали осваивать эту область, и теперь хотим поделиться нашими знаниями и открытиями с вами․ Давайте начнем!

Что такое Компактность?

Прежде чем углубляться в струнные компактные пространства, важно понять, что такое компактность в топологии․ Компактность – это свойство пространства, которое, грубо говоря, означает, что из любой его "бесконечной" коллекции можно выделить "конечную" подколлекцию, которая покрывает все пространство․ Звучит запутанно, не правда ли?

Представьте себе, что у вас есть огромная карта города, и вы хотите отметить на ней все дома․ Компактность означает, что даже если у вас бесконечно много маленьких карт, покрывающих отдельные части города, вы всегда сможете выбрать конечное число этих маленьких карт, которые вместе покроют весь город․ Это очень полезное свойство, которое позволяет нам делать важные выводы о поведении функций и других математических объектов в этих пространствах․

Примеры компактных пространств:

• Замкнутый интервал [a, b] на числовой прямой․
• Окружность․
• Замкнутый шар в n-мерном евклидовом пространстве․

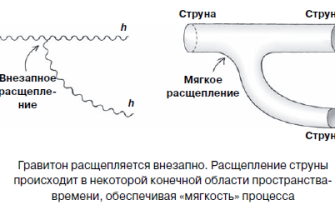
Теперь, когда мы немного разобрались с компактностью, давайте перейдем к струнным пространствам․ В своей основе, струнное пространство – это пространство путей․ Представьте себе, что у вас есть две точки в каком-то другом пространстве, и вы рассматриваете все возможные способы соединить эти две точки линией (или "струной")․ Множество всех этих "струн" и есть струнное пространство․

Более формально, струнное пространство между двумя точками x и y в топологическом пространстве X – это пространство всех непрерывных отображений (или путей) γ: [0, 1] → X таких, что γ(0) = x и γ(1) = y․ Мы можем думать об этих путях как о "струнах", натянутых между точками x и y․

Струнные пространства важны, потому что они позволяют нам изучать свойства исходного пространства X, анализируя свойства этих "струн"․ Например, мы можем исследовать, как меняется форма "струны" при небольших изменениях начальной и конечной точек, или как разные "струны" связаны между собой․

Струнные Компактные Пространства: Соединяем Концепции

Итак, что же такое струнное компактное пространство? Это струнное пространство, которое, как ни странно, является компактным! То есть, если мы возьмем струнное пространство между двумя точками в каком-то другом пространстве, и это струнное пространство окажется компактным, то мы называем его струнным компактным пространством․

Но зачем нам это нужно? Дело в том, что компактность струнного пространства дает нам мощный инструмент для изучения свойств исходного пространства․ Например, если струнное пространство компактно, мы можем использовать теоремы о компактных пространствах, чтобы доказать существование определенных типов "струн" или оценить их длину․ Это может быть полезно во многих областях математики и физики, от теории узлов до квантовой теории поля․

Чтобы лучше понять это, рассмотрим пример․ Представьте себе, что у нас есть компактное пространство X, и мы хотим найти кратчайшую "струну" между двумя точками x и y в X․ Если струнное пространство между x и y компактно, то мы можем использовать теорему о существовании минимума непрерывной функции на компактном множестве, чтобы доказать, что такая кратчайшая "струна" существует․ Это может показаться очевидным, но на самом деле это не всегда так, и компактность струнного пространства играет здесь ключевую роль․

Примеры и Контрпримеры

Чтобы лучше закрепить понимание, давайте рассмотрим несколько примеров и контрпримеров струнных компактных пространств․

Пример 1: Пусть X = [0, 1] – замкнутый интервал на числовой прямой, и пусть x = 0, y = 1․ Тогда струнное пространство между x и y – это пространство всех непрерывных функций γ: [0, 1] → [0, 1] таких, что γ(0) = 0 и γ(1) = 1․ Это струнное пространство является компактным (относительно определенной топологии), поэтому оно является струнным компактным пространством․

Пример 2: Пусть X = ℝ – вся числовая прямая, и пусть x = 0, y = 1․ Тогда струнное пространство между x и y – это пространство всех непрерывных функций γ: [0, 1] → ℝ таких, что γ(0) = 0 и γ(1) = 1․ Это струнное пространство не является компактным, так как мы можем построить последовательность функций, которые "убегают" в бесконечность․

Контрпример: Рассмотрим пространство X = (0,1) ─ открытый интервал․ Хотя сам интервал ограничен, струнное пространство между двумя точками внутри него может не быть компактным, так как последовательность путей может приближаться к границе (0 или 1), не достигая её, и, следовательно, не иметь сходящейся подпоследовательности внутри струнного пространства․

Применение Струнных Компактных Пространств

Струнные компактные пространства находят применение в различных областях математики и физики․ Вот некоторые из них:

1. Теория узлов: Струнные пространства используються для изучения свойств узлов и зацеплений․ Компактность струнного пространства может помочь доказать существование определенных типов узлов или оценить их сложность․
2. Квантовая теория поля: В квантовой теории поля струнные пространства используются для описания траекторий частиц․ Компактность струнного пространства может быть связана с квантованием пространства-времени․
3. Топологический анализ данных: Струнные пространства используются для анализа формы данных․ Компактность струнного пространства может помочь выявить скрытые структуры в данных․

Конечно, это всего лишь несколько примеров, и область применения струнных компактных пространств постоянно расширяется․ Мы уверены, что в будущем они сыграют еще более важную роль в различных областях науки и техники․

Наше путешествие в мир струнных компактных пространств подошло к концу․ Мы надеемся, что смогли немного прояснить эту сложную, но очень интересную область топологии․ Мы рассмотрели основные понятия, привели примеры и контрпримеры, и обсудили некоторые области применения․ Конечно, это всего лишь верхушка айсберга, и впереди еще много неизведанного․ Но мы надеемся, что эта статья вдохновит вас на дальнейшее изучение этой увлекательной темы․

Мы благодарим вас за то, что вы присоединились к нам в этом путешествии․ До новых встреч!

Подробнее

LSI Запрос 1	LSI Запрос 2	LSI Запрос 3	LSI Запрос 4	LSI Запрос 5
Компактные топологические пространства	Определение компактности	Струнное пространство определение	Примеры компактных пространств	Топология струнных пространств
LSI Запрос 6	LSI Запрос 7	LSI Запрос 8	LSI Запрос 9	LSI Запрос 10
Свойства компактных пространств	Применение струнных пространств	Функциональный анализ	Непрерывные отображения	Теорема Тихонова