Струнные Компактные Пространства: Топологическое Путешествие в Бесконечность
Когда мы начинаем погружение в мир топологии‚ нас сразу же окутывает ощущение безграничности и свободы. Это область математики‚ где формы меняются‚ гнутся и растягиваются‚ но сохраняют свои фундаментальные свойства. И сегодня мы отправимся в захватывающее путешествие к одному из самых интересных и интригующих понятий – струнным компактным пространствам. Приготовьтесь‚ будет увлекательно!
Не стоит пугаться сложных терминов. Мы постараемся объяснить все простым и понятным языком‚ чтобы каждый смог прикоснуться к этой красоте. Наша цель – не просто дать определение‚ а рассказать историю‚ показать‚ как эти абстрактные концепции находят применение в реальном мире и почему они так важны для современной науки.
Что такое Компактное Пространство?
Прежде чем углубиться в струнные компактные пространства‚ давайте разберемся с основой – понятием компактности. Представьте себе уютный‚ ограниченный мир‚ в котором все элементы находятся в тесном взаимодействии. В математике это можно представить как пространство‚ из которого нельзя "убежать" в бесконечность.
Формально‚ компактное пространство – это пространство‚ из которого любое открытое покрытие имеет конечное подпокрытие. Звучит немного сложно‚ правда? Давайте упростим. Представьте‚ что у вас есть карта города‚ и вы хотите покрыть ее несколькими кусками ткани (открытыми множествами). Если вы можете покрыть всю карту конечным числом кусков ткани‚ то карта (город) – компактное пространство.
Примеры компактных пространств:
- Отрезок [0‚ 1] на числовой прямой.
- Окружность.
- Квадрат или куб.
Компактность – очень важное свойство‚ поскольку оно позволяет доказывать множество полезных теорем и результатов. Например‚ любая непрерывная функция на компактном пространстве ограничена и достигает своего максимума и минимума.
Теперь‚ когда мы немного разобрались с компактностью‚ давайте перейдем к струнным пространствам. Струнные пространства – это пространства путей‚ соединяющих две точки в некотором пространстве X. Представьте себе‚ что вы хотите добраться из одного города в другой. Существует множество различных маршрутов‚ которые вы можете выбрать. Каждый из этих маршрутов – это "струна" в нашем струнном пространстве.
Более формально‚ струнное пространство между точками x и y в пространстве X – это пространство всех непрерывных функций (путей) γ: [0‚ 1] → X‚ таких что γ(0) = x и γ(1) = y. Мы можем представить каждую такую функцию как "струну"‚ соединяющую точки x и y.
Струнные пространства широко используются в различных областях математики‚ включая:
- Топологию.
- Геометрию.
- Математическую физику.
Струнные Компактные Пространства: Соединяя Точки в Бесконечности
Итак‚ мы подошли к самому главному – струнным компактным пространствам. Это комбинация двух рассмотренных выше понятий: струнных пространств и компактности. Струнное компактное пространство – это струнное пространство‚ которое является компактным.
Но что это означает на практике? Это означает‚ что из любого открытого покрытия струнного пространства можно выделить конечное подпокрытие. Иными словами‚ даже если у нас есть бесконечно много возможных путей между двумя точками‚ мы можем "сжать" их в конечное число "основных" путей‚ которые покрывают все остальные.
Чтобы лучше понять это‚ давайте рассмотрим пример. Представьте себе‚ что у нас есть два города‚ A и B‚ и мы хотим построить между ними дорогу. У нас есть бесконечно много вариантов‚ как это сделать: прямая дорога‚ извилистая дорога‚ дорога с петлями и т.д. Однако‚ если мы потребуем‚ чтобы дорога была "компактной"‚ то есть не уходила слишком далеко от прямой линии между A и B‚ то мы сможем выделить конечное число "основных" дорог‚ которые покрывают все возможные варианты.
"Топология – это наука о непрерывных деформациях‚ о том‚ что остается неизменным при растяжениях‚ сжатиях и скручиваниях." ― Неизвестный математик
Применение Струнных Компактных Пространств
Струнные компактные пространства находят применение в различных областях науки и техники. Вот некоторые примеры:
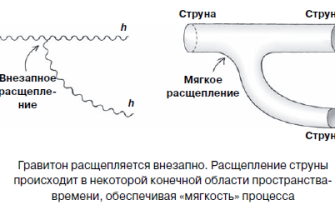
- Теория струн в физике: В теории струн элементарные частицы рассматриваются как одномерные объекты‚ называемые струнами. Струнные компактные пространства используются для описания пространства конфигураций этих струн.
- Робототехника: При планировании движения робота необходимо учитывать множество ограничений‚ таких как избежание препятствий. Струнные компактные пространства могут быть использованы для представления возможных траекторий робота и выбора оптимальной траектории.
- Компьютерная графика: При создании анимации необходимо обеспечить плавное и непрерывное движение объектов. Струнные компактные пространства могут быть использованы для интерполяции между различными положениями объекта и создания реалистичных анимаций.
Примеры и Иллюстрации
Чтобы еще лучше понять концепцию струнных компактных пространств‚ давайте рассмотрим несколько примеров и иллюстраций:
- Отрезок на числовой прямой: Если X – отрезок [0‚ 1]‚ то струнное пространство между точками 0 и 1 – это пространство всех непрерывных функций γ: [0‚ 1] → [0‚ 1]‚ таких что γ(0) = 0 и γ(1) = 1. Это струнное пространство является компактным.
- Окружность: Если X – окружность‚ то струнное пространство между двумя точками на окружности – это пространство всех непрерывных функций γ: [0‚ 1] → окружность‚ таких что γ(0) = x и γ(1) = y. Это струнное пространство также является компактным.
- Пространство петель: Если x = y‚ то струнное пространство называется пространством петель. Пространство петель на компактном пространстве также является компактным.
Наше путешествие в мир струнных компактных пространств подошло к концу. Мы рассмотрели основные понятия‚ дали определение‚ привели примеры и обсудили применение в различных областях. Надеемся‚ что эта статья помогла вам лучше понять эту сложную‚ но увлекательную тему.
Мир топологии полон загадок и открытий. Продолжайте исследовать‚ задавать вопросы и не бояться погружаться в неизведанное. Возможно‚ именно вы сделаете следующее важное открытие в этой области!
Подробнее
| LSI Запрос | LSI Запрос | LSI Запрос | LSI Запрос | LSI Запрос |
|---|---|---|---|---|
| Топология компактных пространств | Определение компактности в топологии | Примеры компактных пространств | Свойства компактных пространств | Струнные пространства в математике |
| Применение струнных пространств | Теория струн и топология | Пути в топологических пространствах | Компактность и непрерывные функции | Струнные пространства и робототехника |