Струны Вселенной: Танцующая Симфония Теории Струн и Вращающейся Динамики

Добро пожаловать, дорогие читатели, в мир, где привычные представления о реальности сталкиваются с захватывающей дух красотой математики и физики! Сегодня мы отправимся в путешествие к самым границам нашего понимания Вселенной, исследуя Теорию Струн и ее динамичные, вращающиеся компоненты. Приготовьтесь, ведь нас ждет захватывающее погружение в мир, где фундаментальные частицы оказываются не точками, а крошечными вибрирующими струнами.

Мы всегда стремились понять, из чего состоит мир. От атомов до кварков, наука постоянно углублялась в поиск фундаментальных строительных блоков материи. Но что, если все, что мы знаем, – лишь верхушка айсберга? Что, если на самом деле вселенная построена из чего-то еще более фундаментального и загадочного?

---

Что такое Теория Струн?

Теория струн – это смелая и элегантная попытка объединить все известные силы природы в рамках единой, всеобъемлющей теории. Она предполагает, что вместо точечных частиц, из которых, как мы считали, состоит материя, вселенная построена из крошечных, вибрирующих струн. Представьте себе гитарные струны, каждая из которых вибрирует на своей частоте, создавая различные ноты. Точно так же, различные моды вибрации струн порождают различные частицы, такие как электроны, кварки и даже гравитоны – гипотетические частицы, переносящие гравитацию.

Основная идея теории струн состоит в том, что разнообразие частиц, наблюдаемых нами в природе, возникает из различных способов, которыми эти крошечные струны могут вибрировать. Подобно тому, как гитарная струна может издавать разные ноты в зависимости от того, как она вибрирует, каждая мода вибрации струны соответствует различной частице с различными свойствами, такими как масса и заряд.

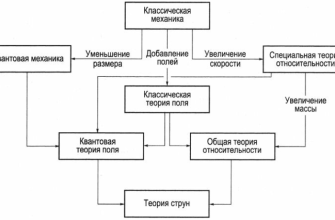
Важно отметить, что теория струн – это не просто красивая математическая конструкция. Она потенциально может решить некоторые из самых глубоких проблем современной физики, такие как объединение общей теории относительности Эйнштейна, описывающей гравитацию, с квантовой механикой, описывающей мир мельчайших частиц. Это объединение оказалось чрезвычайно сложной задачей, поскольку эти две теории описывают мир совершенно разными способами.

---

Вращающиеся Струны: Добавляя Динамику

Первоначально, теория струн возникла как попытка объяснить сильное взаимодействие, связывающее кварки внутри протонов и нейтронов. В этой ранней версии струны представлялись вращающимися объектами. Хотя эта ранняя версия теории струн в конечном итоге была заменена квантовой хромодинамикой (КХД) в качестве основной теории сильного взаимодействия, концепция вращающихся струн оказалась на удивление устойчивой и важной.

Вращение добавляет новый уровень сложности и богатства в теорию струн. Вращающиеся струны могут иметь различные моменты импульса, что приводит к еще большему разнообразию возможных частиц. Это особенно важно, поскольку позволяет теории струн включать частицы с более высокими спинами, которые наблюдаются в природе. Спин – это внутренний момент импульса частицы, и он играет решающую роль в определении ее свойств.

Более того, вращающиеся струны приводят к появлению концепции так называемых "возбужденных состояний". Эти возбужденные состояния соответствуют струнам, вибрирующим и вращающимся с большей энергией. Они могут быть намного массивнее и нестабильнее, чем основные состояния, и могут распадаться на более легкие частицы. Изучение этих возбужденных состояний может дать ценную информацию о структуре и динамике теории струн.

---

Математическая Красота: Формализм и Уравнения

Теория струн – это глубоко математическая теория, и ее понимание требует знания различных математических концепций и методов. Некоторые из ключевых математических инструментов, используемых в теории струн, включают:

• Алгебру Ли: Используется для описания симметрий струн.
• Конформную теорию поля (КТП): Играет решающую роль в описании динамики струн.
• Теорию суперструн: Расширение теории струн, включающее суперсимметрию, которая связывает бозоны и фермионы.
• Матричную теорию: Подход к формулировке теории струн, основанный на матрицах.

Уравнения, описывающие динамику струн, часто сложны и требуют передовых математических методов для решения. Однако, даже без полного понимания математики, можно оценить элегантность и красоту этих уравнений. Они отражают глубокую связь между математикой и физикой и дают представление о фундаментальной природе реальности.

---

Дополнительные Измерения: Необходимость или Фантазия?

Одним из самых интригующих аспектов теории струн является ее требование дополнительных измерений. В отличие от трех пространственных измерений и одного временного измерения, с которыми мы знакомы, теория струн требует как минимум десяти измерений для своей математической согласованности. Это может показаться странным и контринтуитивным, но есть веские причины, по которым дополнительные измерения могут существовать.

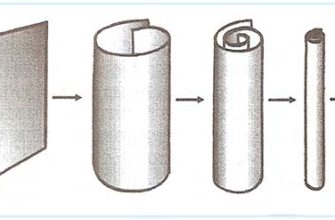
Одна из возможностей состоит в том, что дополнительные измерения свернуты в крошечные, микроскопические пространства, которые мы не можем непосредственно наблюдать. Представьте себе лист бумаги, свернутый в цилиндр. С большого расстояния он кажется одномерным, но при ближайшем рассмотрении вы увидите, что у него есть второе, круговое измерение. Аналогично, дополнительные измерения могут быть свернуты в сложные геометрические формы, известные как многообразия Калаби-Яу, которые слишком малы, чтобы их можно было обнаружить с помощью современных экспериментов.

Другая возможность состоит в том, что мы живем на "бране" – многомерном объекте, встроенном в большее многомерное пространство. В этом сценарии гравитация может распространяться во все измерения, в то время как другие силы природы ограничены браной. Это может объяснить, почему гравитация намного слабее других сил.

---

---

Экспериментальные Подтверждения: Где искать доказательства?

Одним из самых больших вызовов теории струн является отсутствие прямых экспериментальных подтверждений. Из-за крошечного размера струн и высоких энергий, необходимых для их исследования, прямые наблюдения за струнами в настоящее время невозможны. Однако, есть косвенные способы проверки теории струн.

Один из подходов состоит в поиске свидетельств суперсимметрии, которая является предсказанием многих версий теории струн. Суперсимметрия предполагает, что у каждой известной частицы есть партнерская частица с другим спином. Например, у электрона должен быть суперпартнер, называемый "селектрон". Обнаружение суперпартнеров известных частиц стало бы сильной поддержкой теории струн.

Другой подход состоит в поиске свидетельств дополнительных измерений. Если дополнительные измерения действительно существуют, они могут влиять на гравитацию на малых расстояниях. Эксперименты по прецизионному измерению гравитации могут обнаружить эти тонкие эффекты. Кроме того, изучение космического микроволнового фона может дать представление о ранней вселенной и потенциально обнаружить свидетельства дополнительных измерений.

Несмотря на отсутствие прямых экспериментальных подтверждений, теория струн продолжает оставаться мощным и многообещающим инструментом для понимания Вселенной. Ее математическая элегантность и ее способность решать некоторые из самых глубоких проблем современной физики делают ее достойной дальнейшего изучения.

---

Критика и Альтернативные Теории

Теория струн, несмотря на свою популярность, не лишена критики. Некоторые ученые утверждают, что она слишком спекулятивна и не поддается проверке. Другие критикуют ее сложность и отсутствие конкретных предсказаний.

Существуют также альтернативные теории, которые пытаются объединить гравитацию и квантовую механику. Одна из самых известных альтернатив – петлевая квантовая гравитация (ПКГ). ПКГ – это теория, которая квантует само пространство-время. Она предполагает, что пространство-время состоит из дискретных "петель" и "узлов", а не является гладким и непрерывным, как предполагает общая теория относительности.

Другие альтернативные теории включают теорию твисторов, динамическую триангуляцию причинности и теорию асимптотической безопасности. Каждая из этих теорий имеет свои сильные и слабые стороны, и все они находятся в стадии активной разработки.

---

Будущее Теории Струн: Куда мы движемся?

Будущее теории струн остается неопределенным, но многообещающим. С развитием новых математических инструментов и экспериментальных методов мы можем приблизиться к разгадке тайн Вселенной. Теория струн может в конечном итоге привести к революционному прорыву в нашем понимании природы, или она может остаться красивой, но непроверяемой математической конструкцией.

Независимо от того, что нас ждет в будущем, изучение теории струн уже обогатило наше понимание физики и математики. Оно побудило нас мыслить нестандартно и исследовать новые горизонты знаний. И это, пожалуй, самое ценное, что может дать научное исследование.

---

Наше путешествие в мир Теории Струн и вращающейся динамики подошло к концу. Мы исследовали основы теории, ее математическую красоту, ее требование дополнительных измерений и ее экспериментальные проблемы. Мы также рассмотрели критику теории и альтернативные подходы к объединению гравитации и квантовой механики.

Теория струн – это захватывающее и сложное поле исследований, которое продолжает бросать вызов и вдохновлять ученых по всему миру. Независимо от того, окажется ли она в конечном итоге верной теорией всего, она уже оказала глубокое влияние на наше понимание Вселенной. И мы, как пытливые исследователи, продолжаем слушать эту симфонию, пытаясь понять каждый звук, каждую ноту, каждую вибрацию, надеясь однажды постичь полную картину.

Подробнее

Фундаментальные частицы	Квантовая гравитация	Многообразия Калаби-Яу	Суперсимметрия	Космический микроволновый фон
Петлевая квантовая гравитация	Теория твисторов	Динамическая триангуляция	Асимптотическая безопасность	Дополнительные измерения