Теория Струн и Некоммутативная Геометрия: Путешествие в Глубины Реальности

Приветствую вас, дорогие читатели! Сегодня мы отправляемся в захватывающее путешествие в мир теоретической физики, где на стыке математики и физики рождаются самые невероятные идеи о природе нашей Вселенной. Мы поговорим о теории струн и некоммутативной геометрии, двух концепциях, которые, несмотря на свою сложность, предлагают революционный взгляд на структуру реальности. Мы попробуем разобраться, как эти теории связаны между собой и какие приложения они могут иметь для нашего понимания мира.

Наш путь будет непростым, но мы постараемся объяснить сложные вещи простым языком, используя примеры и аналогии, чтобы каждый смог почувствовать себя немного физиком-теоретиком. Приготовьтесь, будет интересно!

Что такое Теория Струн?

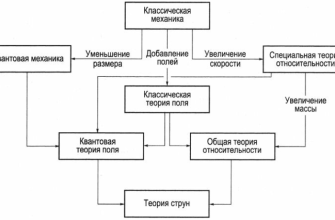
Представьте себе, что вместо точечных частиц, из которых, как нас учили в школе, состоит вся материя, существуют крошечные вибрирующие струны. Именно это лежит в основе теории струн. Каждая струна может вибрировать по-разному, и каждая вибрация соответствует определенной частице – электрону, кварку, фотону и т.д.. Теория струн – это попытка объединить все известные силы и частицы в единую, элегантную теорию "всего". Это амбициозная цель, и именно поэтому теория струн привлекает так много внимания.

Одна из самых привлекательных особенностей теории струн – это её способность естественным образом включать в себя гравитацию, которая традиционно плохо уживается с квантовой механикой. В теории струн гравитон, частица-переносчик гравитационного взаимодействия, является одной из мод вибрации струны. Кроме того, теория струн требует существования дополнительных измерений пространства-времени, помимо тех трех пространственных и одного временного измерения, которые мы наблюдаем в повседневной жизни. Эти дополнительные измерения могут быть свернуты в микроскопические структуры, недоступные для прямого наблюдения.

Ключевые концепции теории струн:

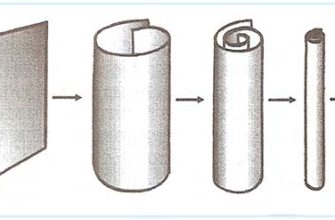
• Многомерность: Теория струн предполагает существование 10 или 11 измерений.
• Компактификация: Дополнительные измерения свернуты в микроскопические пространства Калаби-Яу.
• Суперсимметрия: Связь между бозонами и фермионами.
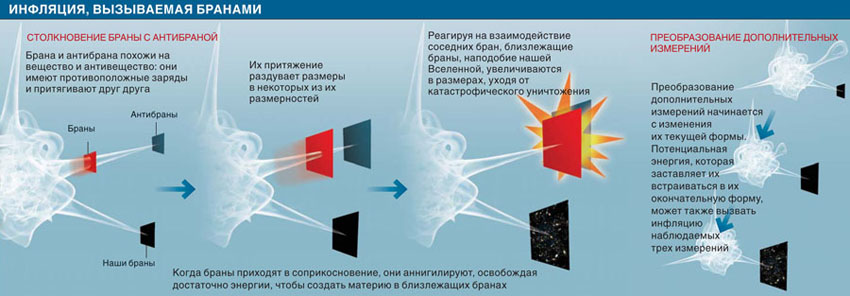
• Браны: Объекты, на которых могут заканчиваться струны.

Некоммутативная Геометрия: Искажение Пространства на Микроуровне

Теперь давайте поговорим о некоммутативной геометрии; В обычной геометрии, которую мы изучали в школе, порядок умножения не имеет значения: 2 * 3 = 3 * 2. Но что, если бы это было не так? Что, если бы порядок, в котором мы измеряем координаты, влиял на результат? Именно это и изучает некоммутативная геометрия.

Она была разработана французским математиком Аленом Конном и представляет собой обобщение обычной геометрии, в котором координаты пространства больше не коммутируют. Это может показаться абстрактным, но представьте себе, что вы пытаетесь определить положение объекта на очень маленьком масштабе, где квантовые эффекты становятся значительными. В этом случае, из-за принципа неопределенности Гейзенберга, вы не можете одновременно точно определить и положение, и импульс частицы. Это означает, что порядок, в котором вы проводите измерения, будет влиять на результат. Некоммутативная геометрия предоставляет математический аппарат для описания таких ситуаций.

Основные идеи некоммутативной геометрии:

• Некоммутативные алгебры: Основной математический инструмент.
• Спектральные тройки: Описание геометрии через алгебру, гильбертово пространство и дираковский оператор.
• Приложения в физике: Моделирование пространства-времени на планковском масштабе.

Связь между Теорией Струн и Некоммутативной Геометрией

Итак, как же связаны эти две, на первый взгляд, разные концепции? Оказывается, связь есть, и она довольно глубокая. Некоммутативная геометрия предоставляет математический язык для описания пространства-времени на очень малых масштабах, где, как предполагается, проявляются эффекты теории струн. В частности, некоторые модели теории струн приводят к эффективным теориям, в которых пространство-время становится некоммутативным.

Представьте себе, что вы рассматриваете струну, движущуюся в магнитном поле. В этом случае координаты конечных точек струны перестают коммутировать. Это означает, что пространство-время, в котором движется струна, становится некоммутативным. Таким образом, некоммутативная геометрия может рассматриваться как эффективное описание теории струн в определенных пределах.

Приложения Теории Струн и Некоммутативной Геометрии

Несмотря на то, что теория струн и некоммутативная геометрия являются очень абстрактными теориями, они имеют потенциальные приложения в различных областях физики и математики.

Приложения в физике:

1. Квантовая гравитация: Теория струн является одним из наиболее перспективных кандидатов на теорию квантовой гравитации.
2. Физика черных дыр: Теория струн может помочь нам понять, что происходит внутри черных дыр.
3. Космология: Теория струн может предложить новые модели ранней Вселенной.
4. Стандартная модель: Теория струн может объяснить параметры Стандартной модели физики элементарных частиц.

Приложения в математике:

1. Топология: Некоммутативная геометрия предоставляет новые инструменты для изучения топологических пространств.
2. Теория чисел: Некоммутативная геометрия может быть применена к изучению дзета-функций и других объектов теории чисел.
3. Алгебра: Некоммутативная геометрия тесно связана с теорией операторных алгебр.

Вызовы и Перспективы

Несмотря на все свои достоинства, теория струн и некоммутативная геометрия сталкиваются с серьезными вызовами. Один из главных вызовов – это отсутствие экспериментальных подтверждений. Энергии, необходимые для проверки предсказаний этих теорий, пока недостижимы на современных ускорителях. Кроме того, математический аппарат этих теорий очень сложен, что затрудняет их развитие.

Тем не менее, мы верим, что эти теории обладают огромным потенциалом. Они предлагают нам совершенно новый взгляд на природу реальности и могут привести к революционным открытиям в будущем. Мы продолжаем исследовать эти теории и надеемся, что в будущем мы сможем найти ответы на многие вопросы, которые они ставят.

Наше путешествие в мир теории струн и некоммутативной геометрии подошло к концу. Мы надеемся, что вы получили удовольствие от этого захватывающего приключения. Мы увидели, как на стыке математики и физики рождаются самые невероятные идеи о природе нашей Вселенной. Мы узнали, что мир может быть гораздо сложнее и интереснее, чем мы себе представляем. И мы надеемся, что это вдохновит вас на дальнейшие исследования и открытия.

Спасибо за внимание!

Подробнее

Квантовая гравитация	Дополнительные измерения	Калаби-Яу	Некоммутативное пространство-время	Суперсимметрия
Браны в теории струн	Алгебра Конна	Спектральные тройки	Принцип неопределенности	Планковская длина

Вот и все.