Теория струн и некоммутативная геометрия: Путешествие к границам реальности

Добро пожаловать, дорогие читатели, в захватывающее путешествие на передовую современной физики! Сегодня мы погрузимся в мир теории струн и некоммутативной геометрии – двух областей, которые, несмотря на свою кажущуюся абстрактность, могут перевернуть наше представление о Вселенной. Мы, как исследователи, всегда стремимся понять фундаментальные законы, управляющие реальностью, и эти теории предлагают нам уникальный взгляд на устройство мироздания.

На первый взгляд, эти концепции могут показаться сложными и непостижимыми. Но не волнуйтесь! Мы постараемся изложить материал максимально доступно, чтобы каждый из вас смог почувствовать себя немного физиком-теоретиком. Мы будем рассказывать о сложных вещах простым языком, опираясь на аналогии и примеры, чтобы помочь вам представить себе мир за пределами привычного опыта.

Что такое теория струн?

Представьте себе, что все, что вы видите вокруг – от крошечных атомов до огромных галактик – состоит не из точечных частиц, как мы привыкли думать, а из крошечных, вибрирующих струн. Это и есть основная идея теории струн. Каждая струна вибрирует с определенной частотой, и эта частота определяет, какую частицу мы наблюдаем. Например, одна частота может соответствовать электрону, другая – фотону, а третья – гравитону (гипотетической частице-переносчике гравитации).

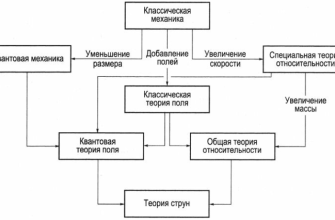
Теория струн возникла как попытка объединить общую теорию относительности Эйнштейна, описывающую гравитацию, и квантовую механику, описывающую мир элементарных частиц. Эти две теории прекрасно работают в своих областях, но когда дело доходит до экстремальных условий, таких как черные дыры или момент Большого взрыва, они приходят в противоречие друг с другом. Теория струн предлагает решение этой проблемы, заменяя точечные частицы протяженными струнами, что позволяет избежать сингулярностей и получить более последовательную картину мира.

Многомерное пространство

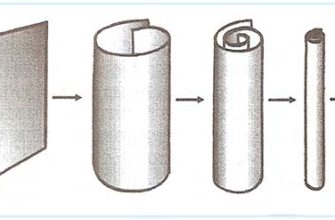
Одной из самых удивительных особенностей теории струн является то, что она требует существования дополнительных измерений пространства-времени. В нашей повседневной жизни мы воспринимаем только три пространственных измерения (длина, ширина, высота) и одно временное. Однако теория струн предполагает, что существует еще шесть или семь дополнительных измерений, свернутых в крошечные, невидимые структуры, известные как многообразия Калаби-Яу. Представьте себе лист бумаги: он имеет два измерения, но если свернуть его в трубочку, то одно измерение станет невидимым для наблюдателя, находящегося на достаточно большом расстоянии.

Эти дополнительные измерения играют важную роль в определении свойств элементарных частиц и фундаментальных сил. Форма и размер многообразий Калаби-Яу влияют на частоты колебаний струн, а значит, и на характеристики частиц, которые мы наблюдаем. Таким образом, теория струн предлагает элегантный способ объяснить разнообразие мира элементарных частиц, исходя из геометрии дополнительных измерений.

Некоммутативная геометрия: Новая перспектива пространства

Теперь давайте переключимся на некоммутативную геометрию – еще одну захватывающую область математики и физики. В обычной геометрии порядок, в котором мы выполняем операции, не имеет значения. Например, если мы сначала повернем объект на 90 градусов, а затем переместим его на 10 сантиметров, результат будет тем же, что и если мы сначала переместим его, а затем повернем. Однако в некоммутативной геометрии это не так. Порядок операций имеет значение, и это приводит к совершенно новым и неожиданным свойствам пространства.

Некоммутативная геометрия возникла как попытка обобщить понятие пространства, включив в него объекты, которые не являются гладкими многообразиями, такие как дискретные пространства или пространства с сингулярностями. Она использует алгебраические методы для описания геометрических объектов, заменяя координаты точек некоммутативными алгебрами. Это позволяет изучать пространства, в которых привычные понятия расстояния и непрерывности теряют свой смысл.

Квантовое пространство-время

Одним из наиболее интересных приложений некоммутативной геометрии является ее связь с квантовой теорией поля и гравитацией. Некоторые физики считают, что на планковском масштабе (около 10^-35 метров) пространство-время перестает быть гладким и непрерывным и приобретает некоммутативную структуру. Это означает, что на этих масштабах порядок, в котором мы измеряем координаты, имеет значение, и это может привести к новым и неожиданным эффектам.

Представьте себе, что вы пытаетесь измерить положение частицы с точностью до планковской длины. В этом случае процесс измерения сам по себе может повлиять на положение частицы, и результат измерения будет зависеть от порядка, в котором вы выполняете измерения. Это похоже на принцип неопределенности Гейзенберга, который утверждает, что мы не можем одновременно точно знать положение и импульс частицы. Некоммутативная геометрия предлагает математический аппарат для описания таких квантовых эффектов в пространстве-времени.

"Самое непостижимое в этом мире — это то, что он постижим." ‒ Альберт Эйнштейн

Приложения теории струн и некоммутативной геометрии

Несмотря на свою абстрактность, теория струн и некоммутативная геометрия имеют потенциальные приложения в различных областях физики и математики. Они могут помочь нам лучше понять природу гравитации, черных дыр, ранней Вселенной и темной материи. Кроме того, они могут привести к новым математическим открытиям и разработкам в области алгебры, геометрии и топологии.

Давайте рассмотрим некоторые конкретные примеры:

Квантовая гравитация: Теория струн является одним из основных кандидатов на роль теории квантовой гравитации, которая объединяет общую теорию относительности и квантовую механику.
Космология: Теория струн может помочь нам понять, что происходило в момент Большого взрыва и как возникла наша Вселенная.
Физика элементарных частиц: Теория струн может объяснить разнообразие элементарных частиц и фундаментальных сил.
Математика: Некоммутативная геометрия привела к новым открытиям в области алгебры, геометрии и топологии.

Актуальные исследования

В настоящее время ученые активно исследуют связь между теорией струн и некоммутативной геометрией. Они пытаются понять, как эти две теории могут дополнять друг друга и привести к более полной и последовательной картине мира. Одним из направлений исследований является изучение некоммутативных струнных теорий, которые объединяют идеи теории струн и некоммутативной геометрии.

Другим направлением является изучение связи между теорией струн и голографическим принципом, который утверждает, что вся информация о трехмерном пространстве может быть закодирована на его двумерной границе. Некоммутативная геометрия может помочь нам понять, как эта информация кодируется и как она связана с квантовой гравитацией.

Будущее теории струн и некоммутативной геометрии

Теория струн и некоммутативная геометрия – это активно развивающиеся области науки, которые находятся на передовой современной физики и математики. Хотя у нас еще нет экспериментальных подтверждений этих теорий, они предлагают нам уникальный и захватывающий взгляд на устройство Вселенной. Мы верим, что в будущем эти теории приведут к новым открытиям и революционным изменениям в нашем понимании мира.

Мы надеемся, что это путешествие в мир теории струн и некоммутативной геометрии было для вас интересным и познавательным. Мы призываем вас продолжать исследовать и изучать эти захватывающие области науки, чтобы вместе с нами открыть новые горизонты знаний.

Подробнее

Теория струн для начинающих	Некоммутативная геометрия простыми словами	Приложения теории струн	Квантовая гравитация и теория струн	Многомерное пространство в физике
Некоммутативное пространство-время	Голографический принцип и теория струн	Современные исследования в теории струн	Математические основы теории струн	Черные дыры и теория струн

Теория струн и некоммутативная геометрия Путешествие к границам реальности