Теория струн и некоммутативная геометрия: Путешествие к границам реальности

Приветствую, друзья! Сегодня мы отправляемся в захватывающее путешествие в мир, где привычные законы физики и геометрии перестают работать. Мы погрузимся в глубины теории струн и некоммутативной геометрии – двух революционных подходов, стремящихся объяснить фундаментальную природу Вселенной. Готовьтесь, будет непросто, но очень интересно! Мы постараемся изложить сложные вещи простым языком, опираясь на наш личный опыт изучения этих тем.

Что такое теория струн?

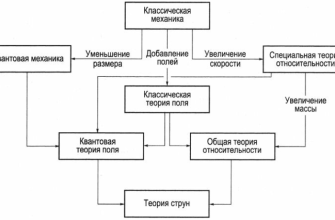
Представьте себе, что все элементарные частицы, из которых состоит наш мир, – это не точечные объекты, а крошечные вибрирующие струны. Именно это лежит в основе теории струн. Каждая мода вибрации струны соответствует определенной частице с ее уникальными свойствами: массой, зарядом, спином. Это как разные ноты, извлекаемые из одной и той же струны музыкального инструмента. Теория струн пытается объединить все известные фундаментальные силы (гравитацию, электромагнетизм, сильное и слабое взаимодействия) в рамках одной элегантной теории.

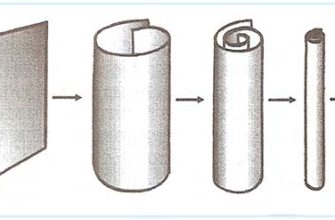
Одно из самых удивительных следствий теории струн – необходимость дополнительных измерений пространства-времени. Вместо привычных нам трех пространственных и одного временного измерения, теория струн требует существования десяти или даже больше измерений! Эти дополнительные измерения, предположительно, свернуты в очень маленькие, недоступные для прямого наблюдения структуры. Звучит как научная фантастика, правда? Но именно это позволяет теории струн избежать математических противоречий и получить физически осмысленные результаты.

Некоммутативная геометрия: геометрия, где порядок имеет значение

В обычной геометрии, которой нас учили в школе, порядок выполнения операций не имеет значения. Например, чтобы добраться из точки А в точку С, можно сначала пройти из А в В, а затем из В в С, или наоборот – результат будет один и тот же. В некоммутативной геометрии все иначе. Здесь порядок действий играет ключевую роль. Это как в алгебре матриц: произведение матриц A x B, как правило, не равно произведению B x A.

Некоммутативная геометрия была разработана французским математиком Аленом Конном для описания пространств, которые не являются гладкими и непрерывными, как привычные нам геометрические объекты. Представьте себе пространство, состоящее из отдельных точек, или пространство с сингулярностями, где обычные методы дифференциальной геометрии не работают. Именно такие "патологические" пространства и призвана описывать некоммутативная геометрия. Она использует алгебраические методы, основанные на некоммутативных алгебрах операторов, для изучения геометрии этих пространств.

Связь между теорией струн и некоммутативной геометрией

Казалось бы, что общего между теорией струн, описывающей фундаментальные частицы, и некоммутативной геометрией, изучающей "плохие" пространства? Оказывается, связь есть, и она довольно глубокая. Во-первых, теория струн сама по себе приводит к появлению некоммутативных структур. Например, в присутствии фонового электромагнитного поля координаты струны могут перестать коммутировать, то есть их порядок в математических выражениях начинает играть роль. Это означает, что пространство-время, в котором движется струна, становится некоммутативным в смысле некоммутативной геометрии.

Во-вторых, некоммутативная геометрия может быть использована для описания компактных дополнительных измерений в теории струн. Вспомните, мы говорили, что теория струн требует существования дополнительных измерений, свернутых в очень маленькие структуры. Эти структуры могут быть настолько малы и сложны, что их описание с помощью обычной геометрии становится невозможным. В этом случае на помощь приходит некоммутативная геометрия, предоставляющая инструменты для изучения таких "квантовых" пространств.

Наш опыт изучения теории струн и некоммутативной геометрии

Мы, как и многие другие энтузиасты, пришли к теории струн и некоммутативной геометрии разными путями. Кто-то увлекся ими, пытаясь понять структуру Вселенной на самых фундаментальных уровнях. Кто-то – в поисках новых математических инструментов для описания сложных физических явлений. Наш опыт был тернистым, но невероятно увлекательным. Мы читали научные статьи, посещали семинары и конференции, обсуждали идеи с коллегами. И, конечно же, сталкивались с трудностями. Понимание сложных математических концепций, визуализация многомерных пространств, освоение новых теоретических методов – все это требовало времени и усилий.

Но самое главное – это чувство восторга и удивления, которое мы испытывали, когда начинали понимать, как все устроено. Когда видишь, как сложные математические структуры отражают глубокие физические закономерности, когда понимаешь, как теория струн и некоммутативная геометрия могут объединить, казалось бы, несовместимые вещи, – это ни с чем не сравнимое ощущение. Это как открыть для себя новый мир, полный тайн и загадок, которые только предстоит разгадать.

Перспективы и вызовы

Теория струн и некоммутативная геометрия – это области науки, находящиеся на переднем крае исследований. Они полны нерешенных проблем и открытых вопросов. Одна из главных проблем – это отсутствие экспериментальных подтверждений теории струн. Энергии, необходимые для проверки предсказаний теории струн, недостижимы на современных ускорителях частиц. Однако ученые ищут косвенные подтверждения, анализируя данные астрономических наблюдений и экспериментов с космическими лучами.

Другая проблема – это математическая сложность теории струн и некоммутативной геометрии. Многие вопросы, связанные с этими теориями, до сих пор не решены математически строго. Однако математики и физики продолжают разрабатывать новые методы и подходы, позволяющие продвинуться в понимании этих теорий. Несмотря на все трудности, перспективы теории струн и некоммутативной геометрии кажутся очень многообещающими. Они могут привести к революции в нашем понимании Вселенной и открыть новые горизонты для науки и техники.

Наше путешествие в мир теории струн и некоммутативной геометрии подошло к концу. Мы надеемся, что смогли хоть немного приоткрыть завесу тайны над этими сложными, но невероятно интересными областями науки. Помните, что наука – это постоянный поиск, сомнения и открытия. Не бойтесь задавать вопросы, исследовать неизведанное и мечтать о невозможном. Возможно, именно вы совершите следующее великое открытие, которое изменит наш мир. Спасибо за внимание!

Подробнее

LSI Запрос 1	LSI Запрос 2	LSI Запрос 3	LSI Запрос 4	LSI Запрос 5
Многомерные пространства	Квантовая гравитация	Стандартная модель	Калибровочные теории	Суперсимметрия
LSI Запрос 6	LSI Запрос 7	LSI Запрос 8	LSI Запрос 9	LSI Запрос 10
Алгебра фон Неймана	Спектральная триада	Компактификация Калаби-Яу	D-браны	Квантование струны

точка.