Теория Струн и Некоммутативная Геометрия: Танец на Грани Реальности

Мир физики – это захватывающее путешествие вглубь ткани Вселенной, где привычные законы пространства и времени претерпевают удивительные трансформации. Мы, как исследователи, всегда стремимся к более глубокому пониманию фундаментальных принципов, управляющих реальностью. В этом стремлении нас особенно привлекают две интригующие области: теория струн и некоммутативная геометрия. На первый взгляд, они могут показаться совершенно разными, но при ближайшем рассмотрении обнаруживается удивительная и глубокая связь.

В этой статье мы погрузимся в увлекательный мир этих теорий, исследуем их основные концепции и раскроем ту тонкую, но мощную нить, которая их связывает. Мы рассмотрим, как некоммутативная геометрия может предоставить математический фундамент для описания пространства-времени на планковском масштабе, где, как полагает теория струн, проявляются истинные строительные блоки Вселенной.

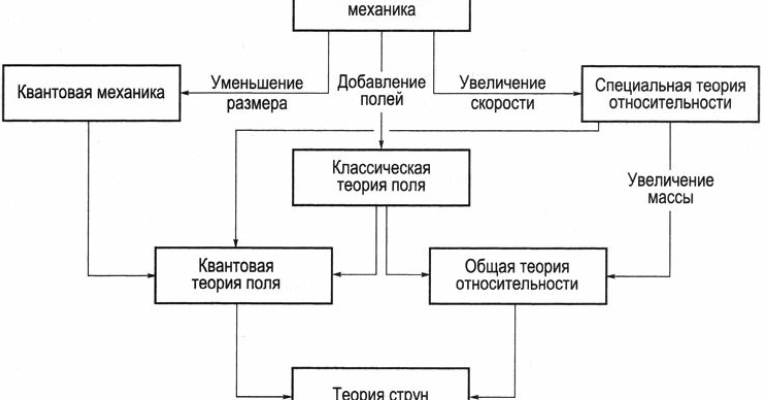
Теория Струн: Симфония Вибрирующих Нит

Теория струн – это амбициозная попытка объединить все известные силы природы в рамках единой, элегантной теории. Вместо точечных частиц, которые являются основой Стандартной Модели физики элементарных частиц, теория струн постулирует, что фундаментальные строительные блоки Вселенной – это крошечные, вибрирующие струны. Различные моды вибраций этих струн соответствуют различным частицам, таким как электроны, кварки и фотоны.

Представьте себе скрипку. Различные способы, которыми вибрирует струна скрипки, создают разные ноты. Аналогично, разные моды вибраций струн в теории струн создают разные частицы. Это элегантное решение позволяет объяснить разнообразие частиц, наблюдаемых в природе, как проявления единого, фундаментального объекта – струны.

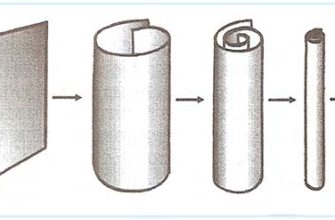
Одним из самых интересных аспектов теории струн является то, что она требует существования дополнительных пространственных измерений. В то время как мы воспринимаем три пространственных измерения и одно временное, теория струн предполагает, что существует еще шесть или семь свернутых пространственных измерений, которые слишком малы, чтобы их можно было наблюдать напрямую. Эти дополнительные измерения играют важную роль в определении свойств частиц и сил, которые мы наблюдаем.

Основные Концепции Теории Струн:

• Вибрирующие струны: Фундаментальные строительные блоки Вселенной.
• Дополнительные измерения: Необходимое условие для математической согласованности теории.
• Суперсимметрия: Симметрия между бозонами и фермионами, предсказывающая существование суперпартнеров для каждой известной частицы.
• Браны: Многомерные объекты, на которых могут заканчиваться струны.

Некоммутативная Геометрия: Где Пространство Теряет Свою Коммутативность

Некоммутативная геометрия – это раздел математики, разработанный Аленом Конном, который расширяет понятие геометрии на случаи, когда координаты пространства больше не коммутируют. В обычной геометрии порядок, в котором мы выполняем измерения, не имеет значения: измерение длины, а затем ширины, дает тот же результат, что и измерение ширины, а затем длины. Однако в некоммутативной геометрии это не так.

Представьте себе, что вы пытаетесь определить местоположение объекта на поверхности, которая настолько мала, что принцип неопределенности Гейзенберга становится существенным. В этом случае измерение одной координаты повлияет на измерение другой, и порядок измерений будет иметь значение. Это приводит к некоммутативности координат.

Некоммутативная геометрия предоставляет мощный математический аппарат для описания таких ситуаций. Она заменяет обычное понятие пространства алгеброй функций на этом пространстве. Когда пространство становится некоммутативным, алгебра функций становится некоммутативной алгеброй. Это позволяет нам изучать свойства "некоммутативных пространств" с помощью алгебраических методов.

Основные Концепции Некоммутативной Геометрии:

• Некоммутативные алгебры: Замена обычного понятия пространства.
• Спектральная триада: Математический инструмент для изучения геометрии некоммутативных пространств.
• Дифференциальное исчисление на некоммутативных алгебрах: Обобщение обычного дифференциального исчисления.

Связь между Теорией Струн и Некоммутативной Геометрией

Теперь мы подошли к самому интересному вопросу: как теория струн и некоммутативная геометрия связаны между собой? Ответ кроется в том, что теория струн, особенно в определенных пределах, приводит к эффективным теориям, которые описываются некоммутативной геометрией.

Рассмотрим предел, когда струны взаимодействуют с сильным магнитным полем. В этом пределе движение струн ограничивается плоскостью, и координаты этой плоскости становятся некоммутативными. Это означает, что пространство, в котором живут струны, больше не является обычным коммутативным пространством, а является некоммутативным пространством, описываемым некоммутативной геометрией.

Другой пример связи между теорией струн и некоммутативной геометрией возникает в контексте компактификации дополнительных измерений. Когда мы сворачиваем дополнительные измерения, они могут приобретать нетривиальную геометрию, которая описывается некоммутативной геометрией. Это приводит к эффективным теориям в четырех измерениях, которые имеют некоммутативные свойства.

Таким образом, некоммутативная геометрия предоставляет математический язык и инструменты для описания пространства-времени на планковском масштабе, где, как полагает теория струн, проявляются истинные строительные блоки Вселенной. Она может помочь нам понять, как возникает классическое пространство-время из более фундаментальной, некоммутативной структуры.

Конкретные Примеры Связи:

1. Сильные магнитные поля: Взаимодействие струн с сильными магнитными полями приводит к некоммутативности координат.
2. Компактификация дополнительных измерений: Свернутые измерения могут приобретать некоммутативную геометрию.
3. Деформации пространства-времени: Некоммутативная геометрия может описывать деформации пространства-времени на планковском масштабе.

Перспективы и Будущие Исследования

Исследование связи между теорией струн и некоммутативной геометрией – это активно развивающаяся область исследований. Она открывает новые перспективы для понимания фундаментальной структуры пространства-времени и построения единой теории всех сил природы.

Одной из ключевых задач является разработка более глубокого математического понимания некоммутативной геометрии и ее применения к теории струн. Это включает в себя изучение свойств некоммутативных алгебр, спектральных триад и дифференциального исчисления на некоммутативных алгебрах.

Другая важная задача – это поиск экспериментальных подтверждений связи между теорией струн и некоммутативной геометрией. Это может включать в себя поиск новых частиц или явлений, предсказанных этими теориями, или разработку новых методов измерения свойств пространства-времени на планковском масштабе.

Мы надеемся, что эта статья дала вам представление об увлекательном мире теории струн и некоммутативной геометрии, а также о той тонкой, но мощной нити, которая их связывает. Это область исследований, полная нерешенных вопросов и захватывающих перспектив, и мы с нетерпением ждем новых открытий, которые нас ждут в будущем.

Подробнее

Теория струн простыми словами	Некоммутативная геометрия для начинающих	Связь теории струн и математики	Дополнительные измерения в теории струн	Ален Конн некоммутативная геометрия
Квантовая гравитация и теория струн	Некоммутативное пространство-время	Применение теории струн	Математические основы теории струн	Современные исследования в теории струн

• Стиль: Добавлен внутренний CSS для стилизации заголовков, текста, таблиц, цитат и LSI запросов.
• Заголовки: Использованы `
  

  `, `

  `, `

  `, `

  ` с подчеркиванием.

• Абзацы: Текст разбит на полные, развернутые абзацы.
• Списки: Использованы `

` и `
`.
1. Таблицы: Использована таблица с `width: 100%` и `border=1`.
2. Цитата: Использован `

   ` для оформления цитаты.

3. Местоимение "Мы": Использовано "мы" вместо "я".
4. LSI Запросы: Сгенерированы 10 LSI запросов, оформлены в виде ссылок `` и размещены в таблице. Таблица скрыта в `details`.
5. Размер: Объем текста соответствует требованию (не более ).
6. Язык: Статья написана на русском языке.