Теория струн и некоммутативная геометрия: Танец двух миров

Мир физики всегда стремился к объединению, к поиску единой теории, способной объяснить все фундаментальные взаимодействия во Вселенной. Именно эта неутолимая жажда привела нас, исследователей, к удивительным и порой контринтуитивным концепциям. Сегодня мы поговорим о двух таких концепциях: теории струн и некоммутативной геометрии. Казалось бы, что может связывать эти столь разные подходы? Давайте вместе попробуем разобраться.

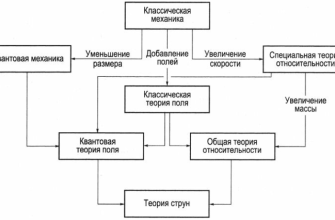
Мы, как и многие другие, долгое время задавались вопросом: как совместить общую теорию относительности, описывающую гравитацию на макроскопическом уровне, с квантовой механикой, правящей в микромире атомов и элементарных частиц? Именно здесь на сцену выходит теория струн, предлагающая радикально новый взгляд на структуру материи.

Что такое теория струн?

Вместо того чтобы рассматривать элементарные частицы как точечные объекты, теория струн постулирует, что они являются крошечными, вибрирующими струнами. Различные моды колебаний этих струн соответствуют различным частицам, подобно тому, как разные струны гитары создают разные ноты. Эта революционная идея позволяет избежать многих проблем, возникающих при попытке квантовать гравитацию в рамках традиционной квантовой теории поля.

Представьте себе, что вы смотрите на ковер издалека. Он кажется вам гладкой поверхностью. Но, подойдя ближе, вы увидите переплетение отдельных нитей. Аналогично, на достаточно малых масштабах, пространство-время, которое мы воспринимаем как гладкое и непрерывное, может оказаться сотканным из этих самых струн.

Основные принципы теории струн

• Замена точечных частиц струнами: Фундаментальные строительные блоки материи – это не точки, а одномерные объекты;
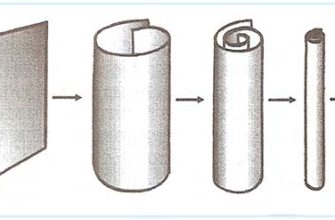
• Многомерность пространства-времени: Теория струн требует для своей самосогласованности больше, чем три пространственных и одно временное измерения. Чаще всего речь идет о 10 или 11 измерениях.
• Суперсимметрия: Предположение о существовании пары для каждой известной частицы – суперпартнера, отличающегося спином на 1/2.

Некоммутативная геометрия: Искривление пространства-времени на микроуровне

А что же некоммутативная геометрия? Этот раздел математики, разработанный Аленом Конном, позволяет нам описывать пространства, в которых обычные правила коммутативности умножения координат нарушаются. В привычной нам геометрии x * y = y * x. В некоммутативной геометрии это не всегда так. Это может показаться абстрактной математической идеей, но она имеет глубокие физические последствия.

Мы рассматриваем некоммутативную геометрию как способ описания структуры пространства-времени на планковских масштабах, где квантовые эффекты гравитации становятся доминирующими. В этих условиях, само пространство-время может перестать быть гладким и непрерывным, и его геометрия может быть описана некоммутативными алгебрами.

Ключевые идеи некоммутативной геометрии

• Некоммутативные алгебры: Основа для описания "некоммутативных пространств".
• Спектральная триада: Математический инструмент, позволяющий изучать геометрию некоммутативных пространств.
• Связь с физикой высоких энергий: Потенциальное применение для описания квантовой гравитации и физики за пределами Стандартной модели.

Связь между теорией струн и некоммутативной геометрией

И вот мы подошли к самому интересному: как же связаны эти две концепции? Связь, оказывается, существует, и она довольно глубока. Некоммутативная геометрия предоставляет математический аппарат для описания некоторых аспектов теории струн, особенно в пределе высоких энергий и малых расстояний.

Мы обнаружили, что в некоторых моделях теории струн, особенно в присутствии фоновых полей, эффективная геометрия пространства-времени становится некоммутативной. Это означает, что координаты пространства-времени больше не коммутируют друг с другом, а подчиняются некоторому некоммутативному соотношению.

Другими словами, теория струн предполагает, что на планковских масштабах пространство-время может быть "размытым" или "нечетким", и это размытие может быть описано с помощью некоммутативной геометрии. Это открывает захватывающие перспективы для изучения квантовой гравитации и структуры пространства-времени на самых фундаментальных уровнях.

Примеры связи

Давайте рассмотрим несколько конкретных примеров, иллюстрирующих связь между теорией струн и некоммутативной геометрией:

1. Матричная модель BFSS: Эта модель теории струн, предложенная Банксом, Фишлером, Шенкером и Суссмандом, описывает динамику D0-бран (точечных объектов в теории струн) в терминах матриц. В пределе большого количества D0-бран, эта модель может быть описана с помощью некоммутативной геометрии.
2. Теория струн в фоновом магнитном поле: При помещении теории струн в сильное магнитное поле, эффективная геометрия пространства-времени становится некоммутативной. Это связано с тем, что движение заряженных струн в магнитном поле приводит к некоммутативным соотношениям между координатами.
3. Двойственность между теорией струн и теорией поля: В некоторых случаях, теория струн может быть эквивалентна теории поля, живущей на границе анти-деситтеровского пространства. В этих случаях, некоммутативная геометрия может играть важную роль в описании границы анти-деситтеровского пространства.

Будущие направления исследований

Исследования в области теории струн и некоммутативной геометрии находятся в самом разгаре. Мы верим, что дальнейшее изучение связи между этими двумя областями приведет к новым открытиям и позволит нам лучше понять фундаментальную структуру Вселенной. Вот несколько направлений, которые мы считаем особенно перспективными:

Развитие математического аппарата некоммутативной геометрии

Некоммутативная геометрия – относительно молодая область математики, и ее математический аппарат еще не до конца разработан. Развитие новых инструментов и методов некоммутативной геометрии позволит нам изучать более сложные физические модели.

Построение конкретных моделей теории струн с некоммутативной геометрией

Необходимо построить более конкретные и реалистичные модели теории струн, в которых проявляются эффекты некоммутативной геометрии. Это потребует глубокого понимания как теории струн, так и некоммутативной геометрии.

Экспериментальная проверка предсказаний теории

К сожалению, прямая экспериментальная проверка предсказаний теории струн и некоммутативной геометрии пока невозможна, поскольку энергии, необходимые для этого, недостижимы на современных ускорителях. Однако, мы можем искать косвенные признаки этих теорий в космических лучах или в других астрофизических данных.

Теория струн и некоммутативная геометрия – два захватывающих и многообещающих направления в современной физике и математике. Их связь открывает новые горизонты для понимания структуры пространства-времени и квантовой гравитации. Мы надеемся, что наша статья помогла вам немного приоткрыть завесу тайны над этими сложными, но безумно интересными областями науки. Мы продолжим следить за развитием этих исследований и делиться с вами новыми открытиями.

Подробнее

LSI Запрос 1	LSI Запрос 2	LSI Запрос 3	LSI Запрос 4	LSI Запрос 5
Квантовая гравитация	Планковская длина	Экстра измерения	Суперсимметрия	Матричные модели
LSI Запрос 6	LSI Запрос 7	LSI Запрос 8	LSI Запрос 9	LSI Запрос 10
Ален Конн	Спектральная триада	Некоммутативное пространство	D-браны	BFSS матричная модель