Теория струн и некоммутативная геометрия: Танец на грани реальности

Мир физики полон удивительных и порой контринтуитивных теорий․ Две из самых захватывающих и сложных – это теория струн и некоммутативная геометрия․ Они кажутся далекими друг от друга‚ как разные галактики‚ но на самом деле‚ они тесно связаны‚ предлагая нам новый взгляд на фундаментальную природу пространства‚ времени и материи․ В этой статье мы погрузимся в эти концепции‚ исследуем их взаимосвязи и попытаемся понять‚ что они значат для нашего понимания Вселенной․

Наше путешествие начнется с основ‚ с того‚ что представляют собой теория струн и некоммутативная геометрия по отдельности․ Затем мы постепенно перейдем к более сложным аспектам‚ где эти две области пересекаются и дополняют друг друга․ Мы будем использовать простые аналогии и примеры‚ чтобы сделать материал более понятным для широкой аудитории‚ не требующей специальной подготовки в области теоретической физики․

Что такое теория струн?

Представьте себе‚ что вместо элементарных частиц‚ таких как электроны и кварки‚ фундаментальными строительными блоками Вселенной являются крошечные‚ вибрирующие струны․ Это и есть основная идея теории струн․ Каждая частота вибрации струны соответствует определенной частице с ее уникальными свойствами‚ такими как масса и заряд․ Вместо множества различных частиц‚ существующих сами по себе‚ мы имеем единый объект – струну – порождающую все многообразие материи и сил․

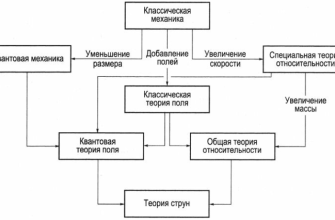
Теория струн возникла как попытка объединить общую теорию относительности Эйнштейна‚ описывающую гравитацию‚ с квантовой механикой‚ описывающей мир элементарных частиц․ Эти две теории прекрасно работают в своих областях‚ но при попытке объединить их возникают серьезные математические противоречия․ Теория струн предлагает решение этой проблемы‚ заменяя точечные частицы струнами‚ что сглаживает сингулярности и позволяет построить последовательную квантовую теорию гравитации․

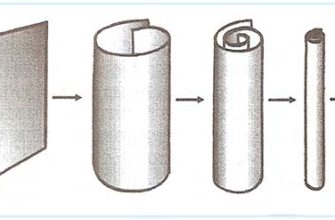
Одним из самых интересных аспектов теории струн является ее требование дополнительных измерений пространства-времени․ В привычном нам трехмерном пространстве и одном измерении времени теория струн не работает․ Для ее математической согласованности необходимо существование 10‚ 11 или даже больше измерений․ Эти дополнительные измерения‚ как полагают‚ свернуты в микроскопические структуры‚ недоступные для непосредственного наблюдения․

Некоммутативная геометрия: Искажение пространства

В обычной геометрии порядок‚ в котором мы выполняем операции‚ не имеет значения․ Например‚ поворот объекта на 90 градусов по часовой стрелке‚ а затем отражение его в зеркале‚ дает тот же результат‚ что и отражение в зеркале‚ а затем поворот․ Однако в некоммутативной геометрии это не так․ Порядок операций влияет на результат‚ что приводит к искажению привычных представлений о пространстве․

Некоммутативная геометрия была разработана французским математиком Аленом Конном как способ обобщения обычной геометрии для описания пространств‚ в которых координаты не коммутируют‚ то есть x * y ≠ y * x․ Это может показаться абстрактной математической концепцией‚ но она имеет глубокие физические приложения‚ особенно в квантовой механике и теории поля․

Представьте себе пространство‚ в котором невозможно точно определить положение частицы․ Чем точнее мы пытаемся определить координату x‚ тем менее точно мы знаем координату y‚ и наоборот․ Это принцип неопределенности Гейзенберга‚ фундаментальный принцип квантовой механики․ Некоммутативная геометрия предоставляет математический аппарат для описания таких "неопределенных" пространств․

Связь между теорией струн и некоммутативной геометрией

И вот мы подошли к самому интересному – к взаимосвязи между теорией струн и некоммутативной геометрией․ Как эти две‚ казалось бы‚ разные области пересекаются и дополняют друг друга?

Оказывается‚ что в определенных режимах теории струн‚ особенно в присутствии фоновых полей‚ пространство-время начинает проявлять некоммутативные свойства․ Это означает‚ что координаты точек в пространстве-времени больше не коммутируют‚ что приводит к искажению геометрии и появлению новых физических явлений․ В этих режимах некоммутативная геометрия становится мощным инструментом для изучения теории струн․

Одним из примеров такой взаимосвязи является описание D-бран․ D-браны – это многомерные объекты‚ на которых могут заканчиваться открытые струны․ В присутствии фонового электромагнитного поля‚ движение открытых струн на D-бране описывается некоммутативной теорией поля․ Это означает‚ что некоммутативная геометрия становится естественным языком для описания физики D-бран․

Более того‚ некоммутативная геометрия может помочь нам понять структуру пространства-времени на планковских масштабах‚ где гравитация становится квантовой и обычные представления о геометрии теряют смысл․ Теория струн предполагает‚ что на этих масштабах пространство-время может быть некоммутативным‚ и некоммутативная геометрия предоставляет инструменты для изучения этой возможности․

Приложения и перспективы

Изучение связи между теорией струн и некоммутативной геометрией имеет множество потенциальных приложений и открывает новые перспективы в физике и математике․ Вот лишь некоторые из них:

• Квантовая гравитация: Некоммутативная геометрия может помочь нам построить последовательную квантовую теорию гравитации‚ объединив общую теорию относительности и квантовую механику․
• Физика элементарных частиц: Некоммутативные теории поля могут описывать новые физические явления‚ не предсказываемые стандартной моделью элементарных частиц․
• Космология: Некоммутативная геометрия может помочь нам понять структуру пространства-времени в ранней Вселенной и природу темной энергии и темной материи․
• Математика: Изучение некоммутативной геометрии приводит к новым математическим открытиям и обобщениям классических геометрических концепций․

Несмотря на значительный прогресс‚ достигнутый в последние годы‚ связь между теорией струн и некоммутативной геометрией остается областью активных исследований․ Многие вопросы остаются без ответа‚ и требуются дальнейшие усилия для полного понимания этой глубокой и сложной взаимосвязи․

Теория струн и некоммутативная геометрия – это две захватывающие и перспективные области физики и математики․ Их взаимосвязь предлагает нам новый взгляд на фундаментальную природу пространства‚ времени и материи‚ открывая новые возможности для понимания Вселенной․ Хотя многие вопросы остаются без ответа‚ исследования в этой области обещают привести к революционным открытиям и изменить наше представление о мире․

Надеемся‚ что наше путешествие в мир теории струн и некоммутативной геометрии было для вас интересным и познавательным․ Мир физики полон загадок‚ и мы продолжаем искать ответы на самые фундаментальные вопросы о природе реальности․

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
Квантовая теория струн	Некоммутативное пространство	D-браны в теории струн	Принцип неопределенности	Квантовая гравитация
Дополнительные измерения	Стандартная модель	Ален Конн геометрия	Темная материя	Планковская длина