Теория струн и некоммутативная геометрия: танго на краю Вселенной

В мире физики, где царят уравнения и строгие формулы, иногда встречаются моменты, когда две, казалось бы, совершенно разные области начинают переплетаться, образуя нечто новое и удивительное. Именно это произошло с теорией струн и некоммутативной геометрией. Мы, простые смертные, не всегда можем понять всю глубину их связи, но можем попытаться прикоснуться к ней, почувствовать её красоту и элегантность.

Представьте себе Вселенную не как гладкое и предсказуемое пространство, а как нечто зернистое, дискретное, где координаты точек не всегда можно поменять местами. Звучит странно, правда? Но именно такие идеи лежат в основе некоммутативной геометрии, и именно они оказались неожиданно полезными для понимания теории струн.

Что такое теория струн?

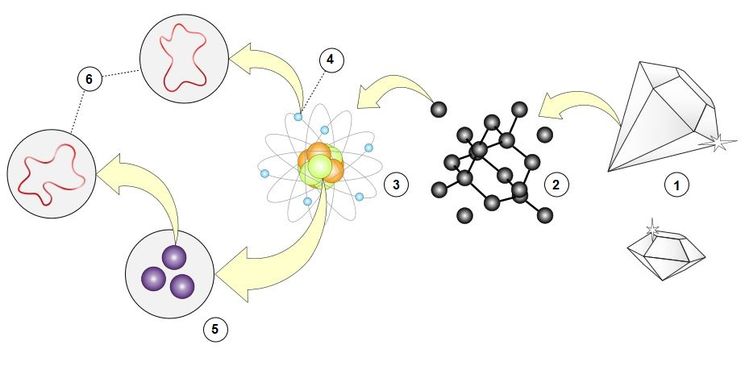
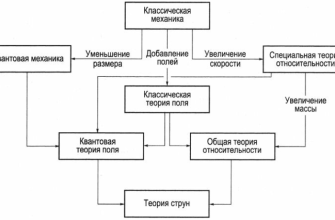
Теория струн – это попытка создать единую теорию всего, объединить общую теорию относительности Эйнштейна, описывающую гравитацию, и квантовую механику, описывающую мир элементарных частиц. Вместо того чтобы рассматривать элементарные частицы как точечные объекты, теория струн предлагает, что они являются крошечными вибрирующими струнами. Разные моды вибраций этих струн соответствуют разным частицам.

• Вибрации: Определяют свойства частиц.
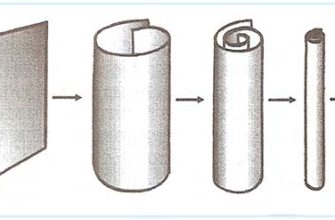
• Многомерность: Требует существования дополнительных измерений пространства.
• Гравитация: Естественно возникает в рамках теории.

Это элегантное решение многих проблем, возникающих при попытке объединить гравитацию и квантовую механику. Однако, теория струн сталкивается с серьезными математическими сложностями и до сих пор не имеет экспериментального подтверждения.

Некоммутативная геометрия: искривление пространства и чисел

Некоммутативная геометрия, разработанная Аленом Конном, является обобщением обычной геометрии, в котором координаты точек пространства не коммутируют, то есть x * y не всегда равно y * x. Это может показаться абстрактной математической концепцией, но она имеет глубокие физические последствия. Представьте себе, что вы пытаетесь измерить положение частицы в пространстве, но сам акт измерения искажает пространство вокруг неё. Это похоже на ситуацию в некоммутативной геометрии.

1. Некоммутативность: Основное отличие от обычной геометрии.
2. Операторы: Заменяют координаты точек.
3. Квантование: Естественно возникает в некоммутативной структуре.

Эта теория позволяет описывать пространства, которые в обычном понимании не являются гладкими или даже непрерывными. Она находит применение в различных областях физики, включая квантовую теорию поля и, как мы увидим, теорию струн.

Как они связаны?

Связь между теорией струн и некоммутативной геометрией возникла неожиданно. Оказалось, что некоторые аспекты теории струн, особенно в пределе низких энергий, могут быть описаны с помощью некоммутативной геометрии. Представьте себе, что струны движутся в пространстве с фоновым магнитным полем. В этом случае эффективная геометрия, которую "видят" струны, становится некоммутативной.

Эта связь открывает новые возможности для изучения теории струн. Некоммутативная геометрия предоставляет мощные математические инструменты для анализа сложных струнных взаимодействий. Более того, она позволяет строить новые модели Вселенной, в которых пространство-время имеет некоммутативную структуру.

Примеры связи

Рассмотрим несколько конкретных примеров, демонстрирующих связь между теорией струн и некоммутативной геометрией:

• D-браны: Эти объекты в теории струн, на которых могут заканчиваться открытые струны, в определенных условиях описываются некоммутативными теориями поля.
• Т-дуальность: Это симметрия в теории струн, которая связывает геометрии с разными радиусами компактификации. В некоммутативной геометрии Т-дуальность проявляется как преобразование между коммутативными и некоммутативными пространствами.
• Матричная теория: Это формулировка теории струн, в которой пространство-время описывается матрицами, что является типичным примером некоммутативной геометрии.

D-браны и некоммутативное пространство

D-браны – это объекты, на которых могут заканчиваться открытые струны. Когда на D-брану действует сильное магнитное поле, координаты открытых струн на этой D-бране перестают коммутировать. Это приводит к тому, что эффективная теория, описывающая динамику D-браны, становится некоммутативной теорией поля. Это один из наиболее ярких примеров связи между теорией струн и некоммутативной геометрией.

Т-дуальность и зеркальная симметрия

Т-дуальность – это симметрия в теории струн, которая связывает две разные геометрии, где одна геометрия имеет радиус компактификации R, а другая – радиус 1/R. Эта симметрия имеет глубокие последствия для понимания структуры пространства-времени. В контексте некоммутативной геометрии, Т-дуальность может быть интерпретирована как преобразование между коммутативным и некоммутативным пространством. Это означает, что геометрия, которую "видят" струны, может меняться от обычной к некоммутативной при изменении радиуса компактификации.

Будущее исследований

Связь между теорией струн и некоммутативной геометрией – это активно развивающаяся область исследований. Мы, как исследователи, продолжаем изучать эту связь, надеясь найти новые ответы на фундаментальные вопросы о природе Вселенной. Какие еще тайны скрывает эта связь? Какие новые модели Вселенной можно построить, используя некоммутативную геометрию? Эти вопросы остаются открытыми и вдохновляют нас на дальнейшие исследования.

Одним из перспективных направлений является изучение роли некоммутативной геометрии в космологии. Может ли она объяснить раннюю Вселенную, инфляцию или темную энергию? Другое направление – это применение некоммутативной геометрии к физике конденсированного состояния. Могут ли некоммутативные эффекты играть роль в новых материалах или топологических фазах материи?

Исследования в этой области требуют глубокого понимания как теории струн, так и некоммутативной геометрии. Они требуют новых математических инструментов и физических интуиций. Но мы уверены, что эти усилия будут вознаграждены новыми открытиями и более глубоким пониманием фундаментальных законов природы.

Теория струн и некоммутативная геометрия – это две сложные и увлекательные области физики и математики. Их связь открывает новые горизонты для понимания структуры Вселенной. Мы, как исследователи, находимся только в начале этого пути, но уверены, что он приведет нас к новым и удивительным открытиям. Будем следить за развитием этих исследований и делиться с вами новыми знаниями.

Надеемся, что эта статья помогла вам немного приблизиться к пониманию этой сложной, но невероятно красивой области науки. Мир физики полон загадок, и мы рады, что можем вместе с вами исследовать их.

Подробнее

Теория струн для начинающих	Некоммутативная геометрия простыми словами	Связь струн и геометрии	D-браны и некоммутативность	Т-дуальность в теории струн
Матричная теория и геометрия	Применение некоммутативной геометрии	Альберт Конн некоммутативная геометрия	Квантовая геометрия	Современные исследования струн