Теория струн и нелинейные уравнения: Путешествие к границам реальности

Добро пожаловать в мир, где привычные законы физики начинают расплываться, а реальность предстает в совершенно новом свете. Сегодня мы отправимся в увлекательное путешествие, чтобы исследовать теорию струн и её тесную связь с нелинейными уравнениями. Это не просто научная тема – это погружение в глубины математики и физики, где рождаются самые смелые идеи о природе Вселенной. Мы расскажем о сложных вещах простым языком, делясь своими размышлениями и открытиями на этом захватывающем пути.

Начнем с того, что теория струн – это попытка объединить все известные нам силы природы в единую, элегантную теорию. Вместо привычных нам точечных частиц, теория струн предполагает, что все фундаментальные составляющие Вселенной – это крошечные вибрирующие струны. Эти струны настолько малы, что мы не можем их увидеть даже с помощью самых мощных микроскопов. Но именно их вибрации определяют свойства частиц, из которых состоит всё вокруг.

Что такое теория струн?

Теория струн, как мы уже упоминали, представляет собой революционный подход к пониманию фундаментальной природы Вселенной. Вместо того чтобы рассматривать элементарные частицы как точечные объекты, она постулирует, что эти частицы являются проявлениями различных колебательных мод крошечных, одномерных объектов, называемых струнами. Представьте себе скрипичную струну: в зависимости от того, как она вибрирует, она издает разные ноты. Аналогично, различные способы вибрации струн в теории струн соответствуют различным элементарным частицам.

Этот подход имеет несколько важных следствий. Во-первых, он потенциально может объединить все известные силы природы – электромагнитную, слабую, сильную и гравитационную – в рамках одной теории. Во-вторых, теория струн требует существования дополнительных измерений пространства-времени, помимо тех трех пространственных и одного временного, которые мы наблюдаем в повседневной жизни. Эти дополнительные измерения могут быть свернуты в очень маленькие, компактифицированные пространства, недоступные для прямого наблюдения.

Ключевые концепции теории струн

• Многомерное пространство: Теория струн предполагает существование 10 или даже 26 измерений пространства-времени.
• Суперсимметрия: Связывает бозоны и фермионы, предполагая, что у каждой частицы есть суперпартнер.
• Браны: Объекты, подобные струнам, но с большим количеством измерений.
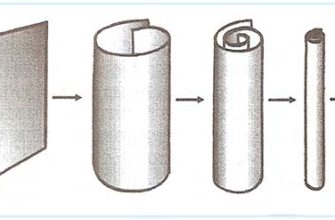
• Компактификация: Процесс "сворачивания" дополнительных измерений, делая их невидимыми для нас.

Нелинейные уравнения и их роль

Нелинейные уравнения играют центральную роль в описании физических явлений, особенно в контексте теории струн. В отличие от линейных уравнений, где принцип суперпозиции выполняется (то есть, сумма двух решений также является решением), нелинейные уравнения описывают системы, где взаимодействие между компонентами системы существенно влияет на её поведение. Это приводит к появлению сложных и часто непредсказуемых явлений, таких как хаос, солитоны и бифуркации.

В теории струн нелинейные уравнения возникают, например, при описании взаимодействия между струнами, а также при рассмотрении динамики пространства-времени в условиях сильной гравитации. Решения этих уравнений могут описывать различные физические объекты, такие как черные дыры, космологические модели и даже сами элементарные частицы. Изучение этих уравнений – это сложная задача, требующая применения самых современных математических методов.

Примеры нелинейных уравнений в теории струн

1. Уравнения Янга-Миллса: Описывают взаимодействие между частицами-переносчиками сил.
2. Уравнения Эйнштейна: Описывают гравитацию как искривление пространства-времени.
3. Уравнения Калаби-Яу: Определяют геометрию дополнительных измерений в теории струн.

Взаимосвязь теории струн и нелинейных уравнений

Теория струн и нелинейные уравнения не просто сосуществуют – они глубоко переплетены между собой. Нелинейные уравнения являются математическим языком, на котором говорит теория струн. Они используются для описания динамики струн, взаимодействия между ними и формирования пространства-времени. Решения этих уравнений позволяют нам заглянуть в самые фундаментальные аспекты Вселенной.

Например, уравнения Эйнштейна, описывающие гравитацию, являются нелинейными. В теории струн они возникают как низкоэнергетическое приближение более фундаментальной теории, описывающей взаимодействие струн. Таким образом, изучение нелинейных уравнений помогает нам понять, как гравитация возникает из более фундаментальных принципов теории струн.

Решения нелинейных уравнений в теории струн

Нахождение решений нелинейных уравнений – это одна из самых сложных задач в математике и физике. В контексте теории струн эта задача становится еще более сложной из-за высокой размерности пространства-времени и сложной природы взаимодействий между струнами. Тем не менее, ученые разработали ряд мощных методов для решения этих уравнений, включая:

• Численные методы: Использование компьютеров для приближенного решения уравнений.
• Аналитические методы: Поиск точных решений уравнений с использованием математических приемов.
• Метод возмущений: Разложение уравнений в ряд и поиск решений в виде последовательных приближений.

Найденные решения позволяют нам изучать различные физические явления, такие как черные дыры, космологические модели и даже свойства элементарных частиц. Они также помогают нам лучше понять саму структуру теории струн и её связь с другими областями физики.

Примеры решений и их интерпретация

Одним из наиболее интересных решений нелинейных уравнений в теории струн является решение, описывающее черную дыру. Это решение показывает, что черная дыра в теории струн – это не просто сингулярность в пространстве-времени, а сложный объект, состоящий из множества струн и бран. Изучение этого решения позволяет нам лучше понять природу черных дыр и их связь с квантовой гравитацией.

Другим важным примером является решение, описывающее космологическую модель. Это решение позволяет нам изучать эволюцию Вселенной на самых ранних этапах её существования и понять, как возникло наше пространство-время. Оно также может помочь нам ответить на вопросы о природе темной материи и темной энергии;

Современные исследования и перспективы

Теория струн и нелинейные уравнения остаются активными областями исследований в современной физике. Ученые по всему миру работают над развитием новых математических методов для решения нелинейных уравнений и применением этих методов к изучению теории струн. Они также пытаются найти экспериментальные подтверждения теории струн, например, с помощью экспериментов на Большом адронном коллайдере.

Перспективы исследований в этой области огромны. Теория струн может привести к революции в нашем понимании Вселенной и открыть новые возможности для развития технологий. Изучение нелинейных уравнений может привести к созданию новых материалов, новых источников энергии и новых способов передачи информации.

Направления исследований

• Разработка новых математических методов для решения нелинейных уравнений.
• Поиск экспериментальных подтверждений теории струн.
• Применение теории струн к изучению космологии и черных дыр.
• Изучение связи теории струн с другими областями физики, такими как квантовая механика и теория поля.

Подробнее

Теория струн для начинающих	Нелинейные уравнения в физике	Решения уравнений Эйнштейна	Суперсимметрия и теория струн	Компактификация дополнительных измерений
Квантовая гравитация и теория струн	Черные дыры в теории струн	Космология струн	Браны и теория струн	Математические методы в теории струн

точка.