Теория струн и нелинейные уравнения: Путешествие вглубь реальности

Мы, как пытливые исследователи, всегда стремимся разгадать тайны Вселенной․ Нас завораживает сложность и элегантность физических законов, управляющих миром․ Одним из самых захватывающих направлений современной физики является теория струн, которая предлагает совершенно новый взгляд на фундаментальную структуру реальности․ В этой статье мы погрузимся в увлекательный мир теории струн и рассмотрим её связь с нелинейными уравнениями, которые играют ключевую роль в описании сложных физических явлений․

Представьте себе, что вместо точечных частиц, из которых, как мы привыкли думать, состоит материя, существуют крошечные вибрирующие струны․ Эти струны, колеблющиеся на различных частотах, порождают различные частицы и силы․ Такова основная идея теории струн, которая обещает объединить все известные силы природы в единую, непротиворечивую теорию․ Однако на пути к этой амбициозной цели стоит множество математических и физических трудностей, в частности, необходимость решения сложных нелинейных уравнений․

Что такое теория струн?

Теория струн – это теоретическая основа, которая пытается объяснить все фундаментальные силы и частицы Вселенной, рассматривая их как различные колебательные моды крошечных одномерных объектов, называемых струнами․ В отличие от стандартной модели физики элементарных частиц, которая рассматривает частицы как точечные объекты, теория струн предполагает, что эти частицы являются проявлениями колебаний струн на микроскопическом уровне․

Одним из ключевых аспектов теории струн является её способность объединять гравитацию с другими фундаментальными силами, такими как электромагнетизм, слабое и сильное взаимодействия․ Это достигается за счет введения гравитона – частицы-переносчика гравитационного взаимодействия – в спектр колебаний струны․ Более того, теория струн требует существования дополнительных измерений пространства-времени, помимо тех четырех (три пространственных и одно временное), которые мы наблюдаем в повседневной жизни․ Эти дополнительные измерения могут быть свернуты в микроскопические структуры, известные как многообразия Калаби-Яу․

Нелинейные уравнения в теории струн

Нелинейные уравнения играют центральную роль в теории струн, поскольку они описывают динамику струн и их взаимодействия․ В отличие от линейных уравнений, где принцип суперпозиции справедлив (то есть сумма двух решений также является решением), нелинейные уравнения не обладают этим свойством․ Это означает, что решения нелинейных уравнений могут быть гораздо более сложными и непредсказуемыми, чем решения линейных уравнений․

Одним из примеров нелинейных уравнений, возникающих в теории струн, являются уравнения движения струны в искривленном пространстве-времени․ Эти уравнения описывают, как струна движется под воздействием гравитационного поля, и они могут быть чрезвычайно сложными для решения․ Другим примером являются уравнения, описывающие взаимодействие струн друг с другом, которые также являются нелинейными и требуют использования сложных математических методов для их анализа․

Примеры нелинейных уравнений в теории струн

• Уравнения Намбу-Гото: Описывают динамику релятивистской струны․
• Уравнения Дирака-Борнера-Инфельда (DBI): Возникают при описании ди-бран – многомерных объектов в теории струн․
• Уравнения супергравитации: Эффективные теории, описывающие низкоэнергетические пределы теории струн․

Решение этих уравнений представляет собой огромную математическую задачу․ Часто приходится прибегать к приближенным методам, численному моделированию и использованию специальных симметрий, чтобы получить хоть какие-то результаты․

Методы решения нелинейных уравнений

В теории струн используются различные методы для решения нелинейных уравнений, в т․ч․:

1. Пертурбативная теория: Этот метод основан на разложении решения по малому параметру, который характеризует силу взаимодействия между струнами․ Однако пертурбативная теория часто оказывается недостаточной для описания сильных взаимодействий и непертурбативных эффектов․
2. Численное моделирование: Компьютерные симуляции позволяют исследовать динамику струн и их взаимодействия в сложных ситуациях, когда аналитические решения недоступны․
3. Интегрируемые модели: Некоторые нелинейные уравнения, возникающие в теории струн, оказываются интегрируемыми, то есть допускают точные аналитические решения․ Изучение этих интегрируемых моделей может дать ценную информацию о структуре и свойствах теории струн․
4. Метод Монте-Карло: Статистический метод, используемый для оценки интегралов и решения уравнений, особенно в многомерных пространствах․

Каждый из этих методов имеет свои преимущества и недостатки, и выбор конкретного метода зависит от конкретной задачи и доступных ресурсов․

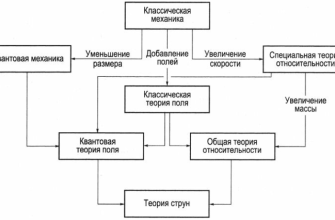
Значение теории струн для физики

Несмотря на то, что теория струн до сих пор не имеет экспериментального подтверждения, она оказала огромное влияние на развитие теоретической физики․ Она привела к новым математическим открытиям, новым взглядам на природу пространства-времени и новым подходам к решению фундаментальных физических проблем․ Теория струн также стимулировала развитие других областей физики, таких как теория поля, теория суперсимметрии и теория супергравитации․

Одной из самых важных заслуг теории струн является её способность объединять гравитацию с квантовой механикой․ Это является одной из самых сложных задач современной физики, и теория струн предлагает одно из наиболее перспективных решений․ Кроме того, теория струн может объяснить происхождение фундаментальных констант природы и предсказать новые частицы и силы, которые могут быть обнаружены в будущем․

Современные исследования и перспективы

В настоящее время теория струн является активной областью исследований, в которой работают тысячи ученых по всему миру․ Они изучают различные аспекты теории струн, разрабатывают новые математические методы и пытаются связать теорию струн с экспериментальными данными․ Одним из самых перспективных направлений исследований является изучение голографического принципа, который связывает теорию струн в пространстве анти-де Ситтера с конформной теорией поля на границе этого пространства․ Этот принцип позволяет изучать свойства теории струн с помощью более простых методов конформной теории поля․

Другим важным направлением исследований является изучение космологических моделей, основанных на теории струн․ Эти модели позволяют объяснить происхождение Вселенной, инфляцию и темную энергию․ Кроме того, ученые пытаются разработать экспериментальные тесты теории струн, которые могли бы подтвердить или опровергнуть её предсказания․ Эти тесты могут включать поиск новых частиц и сил, измерение свойств гравитационных волн и изучение космического микроволнового фона․

Теория струн и нелинейные уравнения – это сложные и захватывающие области современной физики, которые обещают революционизировать наше понимание Вселенной․ Несмотря на то, что на пути к полному пониманию теории струн стоит множество трудностей, мы уверены, что в будущем ученые смогут преодолеть эти трудности и раскрыть все тайны теории струн․ Возможно, именно теория струн станет тем самым "ключом ко всему", который позволит нам понять фундаментальную структуру реальности и место человека во Вселенной․

Мы надеемся, что эта статья дала вам представление о теории струн и её связи с нелинейными уравнениями․ Это лишь краткий обзор огромной и сложной области, и мы призываем вас к дальнейшему изучению этой захватывающей темы․

Подробнее

LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос	LSI Запрос
Многообразия Калаби-Яу	Квантование струны	Динамика струны	Суперсимметрия	Гравитон
Стандартная модель	Экспериментальное подтверждение	Дополнительные измерения	Непертурбативные эффекты	Космология струн