Теория Струн и Нелинейные Уравнения: Путешествие в Глубины Вселенной

Мы, как и многие, всегда были заворожены тайнами Вселенной. От мельчайших частиц до огромных галактик, космос полон загадок, которые человечество пытается разгадать на протяжении веков. Одной из самых захватывающих и перспективных теорий, претендующих на объяснение фундаментальной природы реальности, является теория струн. Вместе с ней мы столкнулись с миром нелинейных уравнений, сложным и запутанным, но невероятно важным для понимания динамики струн и, следовательно, самой Вселенной.

Наше путешествие в эту область началось с любопытства и переросло в глубокое увлечение. Мы читали книги, смотрели лекции, участвовали в обсуждениях и, конечно, пытались разобраться в математических выкладках. Это было непросто, но каждый шаг вперед приносил огромное удовлетворение. В этой статье мы хотим поделиться нашим опытом и попытаться объяснить сложные концепции теории струн и нелинейных уравнений простым и понятным языком.

Что такое Теория Струн?

Начнем с основ. Теория струн, это теоретическая основа, которая пытается объединить все фундаментальные силы природы в единую теорию. В отличие от стандартной модели физики элементарных частиц, которая рассматривает фундаментальные частицы как точечные объекты, теория струн предполагает, что эти частицы на самом деле являются крошечными вибрирующими струнами.

Представьте себе скрипичную струну. В зависимости от того, как она вибрирует, она издает разные ноты. Аналогично, в теории струн разные моды вибрации струн соответствуют разным частицам с разными массами и зарядами. Это элегантное объяснение разнообразия частиц, которые мы наблюдаем в природе.

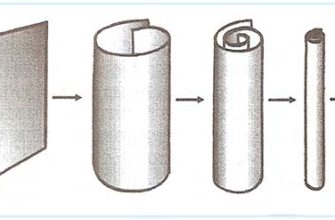
Однако, чтобы теория струн работала, она требует больше измерений, чем те, которые мы видим в повседневной жизни. Стандартная теория предполагает три пространственных измерения и одно временное. Теория струн, в зависимости от ее конкретной версии, требует 10, 11 или даже 26 измерений! Куда делись остальные измерения? Ответ заключается в том, что они свернуты в крошечные, незаметные нам структуры, известные как многообразия Калаби-Яу.

Основные концепции Теории Струн:

• Струны: Фундаментальные объекты, заменяющие точечные частицы.
• Вибрации: Разные моды вибрации струн соответствуют разным частицам.
• Дополнительные измерения: Необходимы для математической согласованности теории.
• Многообразия Калаби-Яу: Компактифицированные дополнительные измерения.

Нелинейные Уравнения и их Роль

Теперь перейдем к нелинейным уравнениям. В отличие от линейных уравнений, где изменение входных данных пропорционально изменению выходных данных, нелинейные уравнения описывают системы, где эта пропорциональность нарушается. Это делает их гораздо более сложными для решения, но также и гораздо более интересными, поскольку они могут описывать широкий спектр сложных явлений.

В контексте теории струн, нелинейные уравнения возникают при описании динамики струн, особенно при их взаимодействии друг с другом; Эти уравнения могут быть невероятно сложными, и часто не существует аналитических решений. Это означает, что нам приходится прибегать к численным методам и компьютерному моделированию, чтобы понять, как струны взаимодействуют и как это взаимодействие влияет на свойства Вселенной.

Одним из ключевых примеров является уравнение Янга-Миллса, которое описывает взаимодействие фундаментальных сил, таких как сильное и слабое взаимодействие. Это уравнение является нелинейным, и его решение представляет собой огромную проблему. Решение уравнения Янга-Миллса также является одной из семи "Задач тысячелетия" Математического института Клэя, за решение которой предлагается приз в миллион долларов.

Примеры Нелинейных Уравнений в Теории Струн:

1. Уравнение Янга-Миллса.
2. Уравнения Эйнштейна (в контексте теории супергравитации, связанной с теорией струн).
3. Уравнения, описывающие динамику D-бран (мембран, на которых могут заканчиваться струны).

Связь между Теорией Струн и Нелинейными Уравнениями

Итак, как же теория струн связана с нелинейными уравнениями? Связь заключается в том, что нелинейные уравнения являются математическим языком, на котором описывается динамика струн и их взаимодействие. Эти уравнения позволяют нам понять, как струны вибрируют, как они взаимодействуют друг с другом и как это взаимодействие влияет на свойства Вселенной.

Например, при изучении взаимодействия двух струн, мы сталкиваемся с нелинейными уравнениями, которые описывают, как эти струны деформируются и перестраиваются во время столкновения. Решение этих уравнений позволяет нам предсказать, какие частицы будут образованы в результате этого взаимодействия.

Кроме того, нелинейные уравнения играют важную роль в изучении космологии в рамках теории струн. Они позволяют нам моделировать раннюю Вселенную и понять, как она развивалась после Большого взрыва. Эти модели могут предсказать существование новых частиц и явлений, которые могут быть обнаружены в будущем.

Решения Нелинейных Уравнений в Теории Струн

Как мы уже упоминали, решение нелинейных уравнений представляет собой огромную проблему. В большинстве случаев аналитические решения не существуют, и нам приходится прибегать к численным методам. Это означает, что мы используем компьютеры для аппроксимации решений уравнений.

Существует множество различных численных методов, которые используются для решения нелинейных уравнений в теории струн. Некоторые из них основаны на методе конечных элементов, другие — на методе конечных разностей. Выбор конкретного метода зависит от конкретной задачи и от доступных вычислительных ресурсов.

Одним из важных направлений исследований является разработка новых и более эффективных численных методов для решения нелинейных уравнений. Это позволит нам изучать более сложные системы и получать более точные результаты. Кроме того, развитие квантовых компьютеров может открыть новые возможности для решения этих уравнений.

Методы решения нелинейных уравнений:

• Численные методы (метод конечных элементов, метод конечных разностей).
• Аналитические методы (в редких случаях, когда это возможно).
• Компьютерное моделирование.

Перспективы и Будущее Исследований

Теория струн и нелинейные уравнения — это области, которые находятся на переднем крае современной физики. Несмотря на то, что мы уже многого достигли, еще многое предстоит узнать. Одной из главных задач является разработка экспериментальных методов, которые могли бы проверить предсказания теории струн.

Например, ученые надеются обнаружить признаки дополнительных измерений или новых частиц, предсказанных теорией струн, в экспериментах на Большом адронном коллайдере (LHC). Кроме того, астрономические наблюдения могут помочь нам понять природу темной материи и темной энергии, которые могут быть связаны с теорией струн.

Развитие квантовых компьютеров также может открыть новые возможности для исследований в этой области. Квантовые компьютеры могут позволить нам решать нелинейные уравнения, которые сейчас недоступны для классических компьютеров. Это может привести к прорывам в нашем понимании фундаментальной природы реальности.

Мы верим, что теория струн и нелинейные уравнения сыграют важную роль в нашем будущем понимании Вселенной. Это сложные и захватывающие области, которые требуют усилий и сотрудничества ученых со всего мира. Мы рады быть частью этого путешествия и надеемся, что эта статья вдохновит вас на дальнейшее изучение этих удивительных тем.

Надеемся, что эта статья была полезной и интересной для вас. Мы призываем вас продолжать исследовать эти удивительные темы и делиться своими знаниями с другими. Вместе мы сможем разгадать тайны Вселенной!

Подробнее

Квантовая гравитация и теория струн	Суперсимметрия в теории струн	Многообразия Калаби-Яу примеры	Численные методы для нелинейных уравнений	Уравнение Янга-Миллса решение
Экспериментальное подтверждение теории струн	Теория струн космология	D-браны в теории струн	Квантовые компьютеры и физика	Фундаментальные силы природы