Теория струн и нелинейные уравнения: Путешествие сквозь кротовые норы математики
Добро пожаловать в удивительный мир, где математика и физика переплетаются в сложном танце, рождая теории, способные перевернуть наше представление о Вселенной; Сегодня мы отправимся в путешествие по теории струн и ее связи с нелинейными уравнениями. Этот путь будет полон загадок, откровений и, конечно же, математических формул. Приготовьтесь, будет интересно!
Наше путешествие начинается с вопроса: что такое теория струн? В двух словах, это попытка объединить все известные нам силы природы в единую, элегантную теорию. Вместо того чтобы рассматривать элементарные частицы как точечные объекты, теория струн предполагает, что они являются крошечными вибрирующими струнами. Эти струны вибрируют на разных частотах, каждая из которых соответствует определенной частице. Представьте себе скрипку, где каждая струна может издавать разные ноты – так и в теории струн каждая струна может "издавать" разные частицы.
Что такое теория струн?
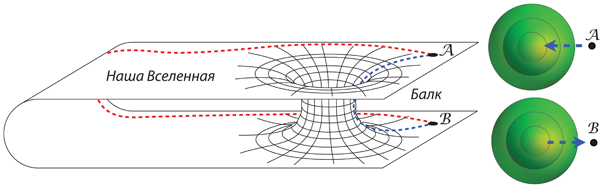
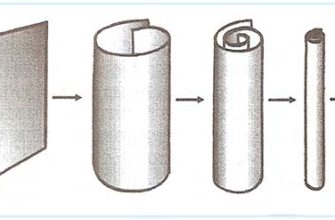
Теория струн – это не просто физическая теория, это целая математическая вселенная. Она требует существования дополнительных измерений пространства-времени, которые мы не воспринимаем в повседневной жизни. Эти измерения свернуты в крошечные структуры, известные как многообразия Калаби-Яу. Представьте себе лист бумаги, свернутый в трубочку – с большого расстояния он выглядит как одномерная линия, но вблизи вы видите, что он имеет два измерения. Так и с дополнительными измерениями в теории струн – они есть, но мы их не видим.
- Заменяет точечные частицы на вибрирующие струны.
- Предполагает существование дополнительных измерений пространства-времени.
- Стремится объединить все известные силы природы.
Но зачем нам вообще нужна теория струн? Дело в том, что существующая Стандартная модель физики элементарных частиц, хотя и очень успешна, имеет свои недостатки. Она не объясняет гравитацию, не дает ответа на вопрос о темной материи и темной энергии, и содержит множество параметров, которые приходится определять экспериментально. Теория струн, в свою очередь, обещает решить все эти проблемы, предоставив единую, фундаментальную теорию всего.
Нелинейные уравнения: Сердце теории струн
Теперь давайте поговорим о нелинейных уравнениях. Что это такое и почему они так важны для теории струн? Нелинейные уравнения – это уравнения, в которых зависимость между переменными не является линейной. Это означает, что если вы удвоите одну переменную, то результат не обязательно удвоится. Такие уравнения часто описывают сложные, хаотические системы, где малые изменения могут приводить к большим последствиям.
В теории струн нелинейные уравнения возникают естественным образом. Они описывают взаимодействие струн друг с другом, а также их взаимодействие с пространством-временем. Решение этих уравнений – задача чрезвычайно сложная, но и чрезвычайно важная. Ведь именно решения нелинейных уравнений позволяют нам понять, как устроена Вселенная на самом фундаментальном уровне.
- Определите нелинейное уравнение, которое описывает динамику струн.
- Найдите решение этого уравнения, которое соответствует определенной физической ситуации.
- Интерпретируйте это решение, чтобы понять, что оно говорит нам о свойствах струн и пространства-времени.
Одним из наиболее известных примеров нелинейных уравнений в теории струн является уравнение Янга-Миллса. Это уравнение описывает взаимодействие фундаментальных частиц, таких как кварки и глюоны, которые являються строительными блоками материи. Решение уравнения Янга-Миллса – одна из семи "задач тысячелетия", за решение которой Математический институт Клэя предлагает приз в размере одного миллиона долларов. Это говорит о том, насколько сложна и важна эта задача.
Примеры нелинейных уравнений в теории струн
Помимо уравнений Янга-Миллса, в теории струн существует множество других нелинейных уравнений, описывающих различные аспекты теории. Например, уравнения Эйнштейна, описывающие гравитацию, также являются нелинейными. В теории струн эти уравнения модифицируются, чтобы учесть эффекты квантовой механики и дополнительных измерений.
Еще одним важным примером являются уравнения Намбу-Гото, описывающие динамику струн в пространстве-времени. Эти уравнения также являются нелинейными и сложными для решения, но их решения позволяют нам понять, как струны двигаются и взаимодействуют друг с другом.
- Уравнения Янга-Миллса (взаимодействие частиц)
- Уравнения Эйнштейна (гравитация)
- Уравнения Намбу-Гото (динамика струн)
Решение этих уравнений требует использования самых современных математических методов, таких как теория возмущений, численные методы и методы интегрируемых систем. Ученые по всему миру работают над тем, чтобы найти новые и более эффективные способы решения нелинейных уравнений в теории струн.
Методы решения нелинейных уравнений
Решение нелинейных уравнений – это искусство, требующее глубоких знаний математики и физики, а также творческого подхода и интуиции. Существует множество различных методов, которые можно использовать для решения нелинейных уравнений, каждый из которых имеет свои преимущества и недостатки.
Одним из наиболее распространенных методов является теория возмущений. Этот метод заключается в том, чтобы представить решение уравнения в виде суммы малых поправок к известному решению. Теория возмущений часто дает хорошие результаты, но она может быть очень трудоемкой и не всегда сходится.
Другим важным методом являются численные методы. Эти методы заключаются в том, чтобы аппроксимировать решение уравнения с помощью компьютера. Численные методы позволяют решать уравнения, которые невозможно решить аналитически, но они требуют больших вычислительных ресурсов и могут быть подвержены ошибкам округления.
Наконец, существуют методы интегрируемых систем. Эти методы основаны на использовании специальных математических структур, которые позволяют находить точные решения нелинейных уравнений. Методы интегрируемых систем очень мощные, но они применимы только к ограниченному классу уравнений.
| Метод | Описание | Преимущества | Недостатки |
|---|---|---|---|
| Теория возмущений | Представление решения в виде суммы малых поправок | Часто дает хорошие результаты | Трудоемкий, не всегда сходится |
| Численные методы | Аппроксимация решения с помощью компьютера | Позволяет решать сложные уравнения | Требует больших вычислительных ресурсов, подвержен ошибкам |
| Методы интегрируемых систем | Использование специальных математических структур | Позволяет находить точные решения | Применим только к ограниченному классу уравнений |
"Самое прекрасное и глубокое переживание, которое может выпасть на долю человека, – это ощущение таинственности. Оно лежит в основе религии и всех наиболее глубоких тенденций в науке." ⸺ Альберт Эйнштейн
Будущее теории струн и нелинейных уравнений
Теория струн и нелинейные уравнения – это две области науки, которые находятся на переднем крае современной физики и математики. Они обещают революционизировать наше понимание Вселенной и предоставить нам новые инструменты для решения самых сложных научных задач.
В будущем мы можем ожидать новых открытий в теории струн, которые позволят нам лучше понять структуру пространства-времени, природу темной материи и темной энергии, а также происхождение Вселенной. Мы также можем ожидать разработки новых и более эффективных методов решения нелинейных уравнений, которые позволят нам решать задачи, которые сейчас кажутся неразрешимыми.
- Более глубокое понимание структуры пространства-времени.
- Объяснение природы темной материи и темной энергии.
- Разработка новых методов решения нелинейных уравнений.
Наше путешествие по теории струн и нелинейным уравнениям подошло к концу. Мы надеемся, что оно было для вас интересным и познавательным. Помните, что наука – это бесконечный поиск истины, и каждый из нас может внести свой вклад в этот поиск.
Подробнее
| Струны и дополнительные измерения | Уравнения Янга-Миллса решения | Квантовая гравитация струны | Нелинейные уравнения физика | Стандартная модель теория струн |
| Теория струн для начинающих | Многообразия Калаби-Яу | Методы решения нелинейных уравнений | Применение теории струн | Теория струн и космология |