Теория Струн и Нелинейные Уравнения: Решения, Открытия и Личный Опыт
Приветствую вас, дорогие читатели! Сегодня мы отправляемся в захватывающее путешествие в мир теоретической физики, где сталкиваются теория струн и нелинейные уравнения. Мы не будем просто пересказывать учебники, а поделимся нашим личным опытом, инсайтами и трудностями, с которыми мы столкнулись, пытаясь разобраться в этих сложных, но невероятно красивых концепциях. Приготовьтесь к погружению в мир многомерных пространств, квантовых флуктуаций и математических головоломок!
Наш путь начался с простого любопытства. Нас всегда завораживала идея единой теории, способной описать все фундаментальные силы природы. Теория струн казалась наиболее перспективным кандидатом, но чем глубже мы погружались, тем больше вопросов возникало. Нелинейные уравнения, с их кажущейся хаотичностью и сложностью, стали для нас настоящим вызовом. Но, как говорится, "дорогу осилит идущий", и мы решили не сдаваться.
Теория струн – это теоретическая основа, которая предполагает, что фундаментальные частицы, такие как электроны и кварки, на самом деле являются не точечными объектами, а крошечными вибрирующими струнами. Различные моды вибрации этих струн соответствуют различным частицам и силам. Это элегантное решение многих проблем, стоящих перед физикой элементарных частиц, таких как проблема квантовой гравитации.
Однако, теория струн не лишена своих сложностей. Одна из главных – это необходимость существования дополнительных измерений пространства-времени. Вместо привычных нам трех измерений пространства и одного измерения времени, теория струн требует, как минимум, десяти измерений. Как эти дополнительные измерения влияют на наш мир? Как их обнаружить? Эти вопросы до сих пор остаются предметом активных исследований.
- Основные принципы теории струн
- Пространство Калаби-Яу
- Суперсимметрия и суперструны
Нелинейные Уравнения: Хаос и Порядок
Нелинейные уравнения – это математические выражения, в которых зависимость между переменными не является линейной. Это означает, что изменение одной переменной не приводит к пропорциональному изменению другой. Нелинейные уравнения описывают широкий спектр явлений в природе, от турбулентности жидкости до динамики популяций. Они также играют важную роль в теории струн, где описывают взаимодействие струн и геометрию пространства-времени.
Решение нелинейных уравнений – задача нетривиальная. В отличие от линейных уравнений, для них не существует общих методов решения. Каждое уравнение требует индивидуального подхода, часто с использованием численных методов и компьютерного моделирования. Нам приходилось часами сидеть над кодом, пытаясь найти хоть какое-то решение, которое имело бы физический смысл.
- Примеры нелинейных уравнений (уравнение Кортевега — де Фриза, уравнение sine-Gordon)
- Методы решения нелинейных уравнений
- Применение нелинейных уравнений в физике
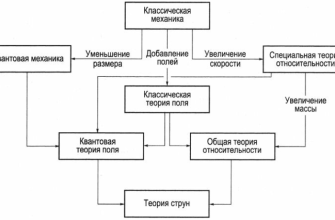
Связь между Теорией Струн и Нелинейными Уравнениями
Казалось бы, что общего между теорией струн, с ее многомерным пространством и квантовыми флуктуациями, и нелинейными уравнениями, описывающими хаотичные системы? На самом деле, связь между ними очень глубокая; Нелинейные уравнения возникают при описании динамики струн и взаимодействия между ними. Они также играют важную роль в теории суперсимметрии, которая является неотъемлемой частью теории струн.
Например, уравнение Кортевега — де Фриза (KdV) описывает распространение солитонов – устойчивых волн, которые не меняют свою форму при распространении. Это уравнение возникает при изучении низкоэнергетических возбуждений в некоторых моделях теории струн. Другие нелинейные уравнения, такие как уравнение sine-Gordon, также находят применение в теории струн при описании различных физических явлений.
Решения и Личный Опыт
Наш личный опыт работы с теорией струн и нелинейными уравнениями был полон взлетов и падений. Мы сталкивались с трудностями при изучении сложных математических концепций, при написании кода для численного моделирования, и при интерпретации полученных результатов. Но каждый раз, когда нам удавалось найти решение, мы испытывали огромное удовлетворение. Это было похоже на открытие новой грани реальности, на прикосновение к тайнам Вселенной.
Одним из самых интересных моментов было изучение солитонных решений нелинейных уравнений. Мы обнаружили, что эти решения описывают не только распространение волн, но и могут быть связаны с образованием черных дыр и другими экзотическими объектами. Это открыло для нас новые перспективы в исследовании связи между теорией струн и гравитацией.
"Невозможно решить проблему, находясь на том же уровне мышления, на котором она была создана." ⎻ Альберт Эйнштейн
Трудности и Преодоления
Работа с теорией струн и нелинейными уравнениями сопряжена с рядом трудностей. Во-первых, это высокий уровень математической подготовки, который требуется для понимания основных концепций. Во-вторых, это необходимость использования численных методов и компьютерного моделирования, что требует знания программирования и умения работать с специализированным программным обеспечением. В-третьих, это сложность интерпретации полученных результатов и их сопоставления с экспериментальными данными.
Мы преодолевали эти трудности, постоянно учась и обмениваясь опытом с коллегами. Мы посещали конференции и семинары, читали научные статьи и книги, и не боялись задавать вопросы. Мы также активно использовали онлайн-ресурсы и форумы, где могли найти ответы на свои вопросы и получить помощь от других исследователей. Самое главное – это не терять энтузиазм и веру в свои силы.
Перспективы и Будущие Исследования
Теория струн и нелинейные уравнения – это области науки, которые продолжают активно развиваться. Впереди нас ждет еще много открытий и новых вызовов. Одним из самых перспективных направлений является разработка новых математических методов для решения нелинейных уравнений. Это позволит нам более глубоко понять динамику струн и их взаимодействие, а также исследовать связь между теорией струн и другими областями физики, такими как космология и физика конденсированного состояния.
Другим важным направлением является разработка экспериментальных методов для проверки предсказаний теории струн. Это сложная задача, так как эффекты теории струн проявляются на очень малых масштабах и при очень высоких энергиях. Однако, с развитием новых технологий и экспериментальных установок, у нас появляется все больше шансов на то, чтобы обнаружить признаки существования дополнительных измерений и других экзотических явлений, предсказанных теорией струн.
Подробнее
| Теория струн для начинающих | Нелинейные уравнения в физике | Решение уравнений КдФ | Дополнительные измерения в теории струн | Квантовая гравитация и струны |
|---|---|---|---|---|
| Суперсимметрия в теории струн | Пространство Калаби-Яу | Численные методы для нелинейных уравнений | Физика элементарных частиц и струны | Солитоны и теория струн |