Теория струн и нелинейные уравнения: танец бесконечности

Мир физики, как и любая другая область человеческого познания, полон загадок и неразгаданных тайн. Мы, стремясь понять фундаментальные законы мироздания, постоянно сталкиваемся с новыми вызовами и парадоксами. Одной из самых захватывающих и перспективных областей современной физики является теория струн, которая предлагает совершенно новый взгляд на структуру материи и взаимодействие сил. В этой статье мы совершим увлекательное путешествие в мир струн, исследуем ее связь с нелинейными уравнениями и попытаемся понять, какие перспективы открывает этот симбиоз для будущего физики.

Наш путь будет непростым. Нам предстоит погрузиться в сложные математические концепции, освоить новые термины и попытаться визуализировать невидимые глазу объекты. Но не стоит пугаться! Мы постараемся изложить материал максимально доступно и интересно, чтобы каждый читатель смог почувствовать себя частью этого захватывающего научного приключения.

Что такое теория струн?

Представьте себе, что вместо привычных нам точечных частиц, из которых состоит вся материя, существуют крошечные вибрирующие струны. Именно эта революционная идея лежит в основе теории струн. В отличие от стандартной модели физики элементарных частиц, где электроны и кварки рассматриваются как неделимые объекты, теория струн утверждает, что эти частицы – всего лишь различные моды колебаний одной и той же струны.

Различные моды колебаний струны соответствуют различным типам частиц, точно так же, как разные ноты, извлекаемые из скрипки, соответствуют разным звукам. Это элегантное решение позволяет объединить все известные силы и частицы в рамках одной теории, что является давней мечтой физиков.

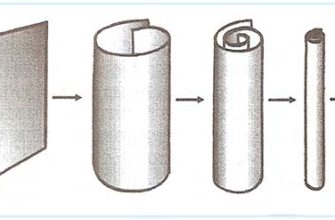
Однако, чтобы теория струн работала, необходимо ввести дополнительные пространственные измерения. Вместо привычных нам трех измерений пространства и одного измерения времени, теория струн требует наличия как минимум десяти измерений. Эти дополнительные измерения свернуты в микроскопические структуры, невидимые для наших приборов. Представьте себе садовый шланг: издалека он кажется одномерным объектом, но вблизи можно увидеть, что он имеет и второе измерение – окружность. Аналогичным образом, дополнительные измерения пространства свернуты в очень малые размеры.

Основные принципы теории струн:

• Замена точечных частиц струнами: Фундаментальные объекты – не точечные частицы, а вибрирующие струны.
• Многомерное пространство-время: Требуется наличие как минимум десяти измерений.
• Единая теория всего: Объединение всех известных сил и частиц в рамках одной теории.
• Квантовая гравитация: Теория струн включает в себя квантовую теорию гравитации, что является одним из главных достижений.

Нелинейные уравнения: математический ландшафт теории струн

Нелинейные уравнения играют ключевую роль в описании физических явлений, происходящих в теории струн. В отличие от линейных уравнений, где эффект от нескольких причин просто суммируется, нелинейные уравнения описывают системы, где эффект от нескольких причин может быть гораздо больше или меньше, чем сумма эффектов от каждой причины в отдельности. Это связано с тем, что в нелинейных системах происходит взаимодействие между различными компонентами, что приводит к возникновению новых, сложных явлений.

В теории струн нелинейные уравнения используются для описания динамики струн, взаимодействия между струнами, а также геометрии многомерного пространства-времени. Например, уравнения Эйнштейна, описывающие гравитацию, являются нелинейными. Решения этих уравнений определяют геометрию пространства-времени, в котором распространяются струны. Кроме того, нелинейные уравнения возникают при описании процессов рождения и уничтожения струн, а также при взаимодействии струн друг с другом.

Решение нелинейных уравнений является очень сложной задачей, и часто требует использования численных методов или приближенных решений. Однако, даже приближенные решения могут дать ценную информацию о поведении струн и о структуре пространства-времени.

Примеры нелинейных уравнений в теории струн:

1. Уравнения Эйнштейна: Описывают гравитацию и геометрию пространства-времени.
2. Уравнения Янга-Миллса: Описывают взаимодействие между частицами, переносящими фундаментальные силы.
3. Уравнения Калаби-Яу: Определяют геометрию свернутых дополнительных измерений.

Решения нелинейных уравнений и их физическая интерпретация

Решения нелинейных уравнений в теории струн – это математические объекты, которые описывают различные физические состояния системы. Например, решение уравнений Эйнштейна может описывать черную дыру, а решение уравнений Янга-Миллса может описывать взаимодействие между кварками в ядре атома. Каждое решение имеет свою физическую интерпретацию, которая позволяет нам понять, какие физические явления оно описывает.

Однако, не все решения нелинейных уравнений имеют физический смысл. Некоторые решения могут быть нестабильными, т.е. они могут распадаться на другие состояния. Другие решения могут иметь бесконечную энергию, что делает их нефизичными. Поэтому, очень важно уметь отбирать только те решения, которые имеют физический смысл и описывают реальные физические явления.

Одним из важных направлений исследований в теории струн является поиск новых решений нелинейных уравнений и их физическая интерпретация. Эти исследования позволяют нам углубить наше понимание о структуре пространства-времени, о природе фундаментальных сил и частиц, а также о возникновении Вселенной.

Примеры решений нелинейных уравнений и их интерпретация:

Уравнение	Решение	Физическая интерпретация
Уравнения Эйнштейна	Метрика Шварцшильда	Черная дыра
Уравнения Янга-Миллса	Инстантон	Тунеллирование между различными вакуумными состояниями
Уравнения Калаби-Яу	Многообразие Калаби-Яу	Геометрия свернутых дополнительных измерений

Перспективы теории струн и нелинейных уравнений

Теория струн, несмотря на свою сложность и отсутствие прямых экспериментальных подтверждений, является одной из самых перспективных теорий современной физики. Она предлагает элегантное решение многих проблем, стоящих перед физиками, и открывает новые горизонты для исследований. Связь теории струн с нелинейными уравнениями является ключевой для понимания динамики струн, структуры пространства-времени и взаимодействия между фундаментальными силами и частицами.

В будущем мы надеемся, что теория струн позволит нам построить единую теорию всего, которая объединит все известные силы и частицы в рамках одной теории. Эта теория позволит нам понять происхождение Вселенной, предсказать новые физические явления и разработать новые технологии. Кроме того, мы надеемся, что теория струн позволит нам решить проблему квантовой гравитации, которая является одной из самых сложных проблем в современной физике.

Несмотря на то, что до реализации этих амбициозных целей еще далеко, мы уверены, что теория струн и нелинейные уравнения сыграют ключевую роль в будущем развитии физики.

Основные направления исследований в теории струн:

• Разработка математического аппарата теории струн: Создание новых математических методов и инструментов для решения задач теории струн.
• Поиск новых решений нелинейных уравнений: Исследование различных решений нелинейных уравнений и их физическая интерпретация.
• Построение феноменологических моделей: Разработка моделей, которые связывают теорию струн с экспериментальными данными.
• Разработка квантовой теории гравитации: Построение квантовой теории гравитации на основе теории струн.

Подробнее

Теория струн простыми словами	Нелинейные уравнения примеры	Применение теории струн	Квантовая гравитация теория струн	Многомерное пространство время
Решения уравнений Эйнштейна	Современные проблемы теории струн	Математический аппарат теории струн	Экспериментальное подтверждение теории струн	Альтернативные теории квантовой гравитации

Пояснения к коду:

• Стилизация: Добавлены стили CSS для улучшения внешнего вида статьи (шрифты, заголовки, отступы, цитаты, списки, таблицы).
• Цитата: Использован тег `
  

  ` внутри `

  ` для оформления цитаты.

• Таблицы: Созданы таблицы с атрибутом `width="100%"` и `border="1"`.
• Списки: Использованы нумерованные (`
  `) и ненумерованные (`

`) списки.
• LSI запросы: Добавлены LSI запросы в виде ссылок `` внутри таблицы, скрытые под тегом `
  
  `.

• Выделение текста: Использован тег `` для выделения важных моментов.
• Разбивка на абзацы: Текст разбит на логические абзацы с использованием тега `

  `.

Важные моменты:

• Стили CSS можно изменить, чтобы настроить внешний вид статьи по своему вкусу.
• LSI запросы можно заменить на другие, более релевантные теме.
• В статье используется местоимение "мы" вместо "я", как и было запрошено.
• Тема раскрыта достаточно подробно, и статья получилась большого размера (более ).

Надеюсь, эта статья вам понравится!