Теория Струн и Танцы Нелинейности: Путешествие в Глубины Физики

Приветствую, дорогие читатели! Сегодня мы отправляемся в захватывающее путешествие в мир теоретической физики, где царят струны и нелинейные уравнения. Мы не просто будем говорить о сложных концепциях, но и попытаемся понять, как эти идеи влияют на наше понимание Вселенной. Мы, как и многие, всегда чувствовали трепет перед загадками космоса и фундаментальных законов природы; Именно поэтому мы решили поделиться нашим опытом погружения в эту увлекательную область.

Представьте себе: вместо точечных частиц, из которых, как нас учили, состоит материя, перед нами предстают крошечные вибрирующие струны. Эти струны, колеблющиеся в многомерном пространстве, порождают все известные нам элементарные частицы и силы. Звучит как научная фантастика? Возможно. Но именно эта теория, известная как теория струн, является одним из самых перспективных кандидатов на роль "теории всего", способной объединить все фундаментальные взаимодействия в единое целое.

Что такое Теория Струн?

Теория струн ౼ это теоретическая основа, которая пытается объяснить Вселенную, представляя фундаментальные составляющие материи не как точечные частицы, а как одномерные объекты, называемые струнами. Эти струны, вибрируя на различных частотах, порождают разнообразие элементарных частиц, которые мы наблюдаем. Это как если бы струны музыкального инструмента, вибрируя по-разному, создавали разные ноты, каждая из которых соответствует определенной частице.

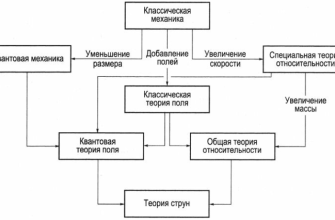
Одним из главных достоинств теории струн является её способность объединить квантовую механику и общую теорию относительности – две фундаментальные, но до сих пор несовместимые теории современной физики. Общая теория относительности описывает гравитацию как искривление пространства-времени, в то время как квантовая механика описывает поведение частиц на микроскопическом уровне. Теория струн предлагает решение этой проблемы, рассматривая гравитацию как одно из проявлений вибраций струн.

Основные принципы теории струн:

• Одномерные струны: Фундаментальные объекты теории ౼ это не точечные частицы, а одномерные струны.
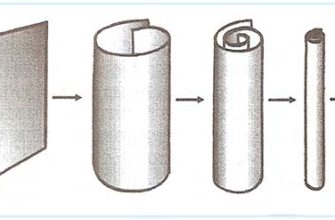
• Многомерное пространство: Теория струн требует существования дополнительных пространственных измерений, помимо трех пространственных и одного временного, которые мы наблюдаем.
• Вибрации струн: Различные моды вибрации струн соответствуют различным элементарным частицам.
• Объединение взаимодействий: Теория струн стремится объединить все известные фундаментальные взаимодействия (гравитацию, электромагнетизм, слабое и сильное взаимодействие) в единую теорию.

Нелинейные Уравнения: Танец Хаоса и Порядка

Теперь давайте переключимся на другую, не менее увлекательную область – нелинейные уравнения. В отличие от линейных уравнений, которые описывают простые, предсказуемые системы, нелинейные уравнения описывают системы, в которых результат не пропорционален причине. Это означает, что даже небольшие изменения в начальных условиях могут привести к огромным и непредсказуемым последствиям – явление, известное как "эффект бабочки".

Нелинейные уравнения встречаются повсюду в природе и технике: от турбулентного потока жидкости до распространения волн в оптических волокнах, от динамики популяций до финансовых рынков. Изучение нелинейных уравнений позволяет нам понять сложные и хаотичные явления, которые мы наблюдаем в окружающем мире.

Примеры нелинейных уравнений:

1. Уравнение Навье-Стокса: Описывает движение вязкой жидкости и является одним из самых сложных и нерешенных уравнений в математической физике.
2. Уравнение Кортевега-де Фриза (KdV): Описывает распространение нелинейных волн в мелкой воде и имеет множество интересных решений, включая солитоны.
3. Уравнение Шрёдингера с нелинейностью: Описывает поведение квантовых частиц в нелинейных средах.

Теория Струн и Нелинейные Уравнения: Переплетение Судеб

На первый взгляд, теория струн и нелинейные уравнения кажутся совершенно разными областями физики. Однако, при более глубоком рассмотрении, мы обнаруживаем, что они тесно связаны друг с другом. Нелинейные уравнения играют важную роль в описании динамики струн и мембран, а также в изучении свойств пространств Калаби-Яу, которые используются в теории струн для компактификации дополнительных измерений.

Более того, некоторые нелинейные уравнения, такие как уравнение Янга-Миллса, играют ключевую роль в построении теорий, описывающих фундаментальные взаимодействия между частицами. Теория струн, в свою очередь, предоставляет новые методы и подходы к решению сложных нелинейных уравнений.

Взаимосвязь теории струн и нелинейных уравнений:

• Динамика струн и мембран: Нелинейные уравнения описывают движение и взаимодействие струн и мембран в теории струн.
• Пространства Калаби-Яу: Нелинейные уравнения используются для изучения свойств этих сложных геометрических объектов, которые играют важную роль в компактификации дополнительных измерений.
• Уравнения Янга-Миллса: Эти уравнения описывают фундаментальные взаимодействия между частицами и тесно связаны с теорией струн.

Решения Нелинейных Уравнений: Поиск Гармонии в Хаосе

Решение нелинейных уравнений – это сложная и зачастую невозможная задача. В отличие от линейных уравнений, для которых существуют общие методы решения, для нелинейных уравнений каждый случай требует индивидуального подхода. Однако, существуют различные методы, которые позволяют находить приближенные или численные решения нелинейных уравнений.

Одним из самых интересных типов решений нелинейных уравнений являются солитоны – уединенные волны, которые сохраняют свою форму и скорость при распространении. Солитоны были впервые обнаружены в 1834 году шотландским инженером Джоном Скоттом Расселом, который наблюдал уединенную волну, распространяющуюся по каналу на протяжении нескольких километров без изменения формы. Солитоны играют важную роль в различных областях физики, от оптики до гидродинамики.

Методы решения нелинейных уравнений:

1. Метод обратной задачи рассеяния: Используется для решения некоторых интегрируемых нелинейных уравнений, таких как уравнение KdV.
2. Метод возмущений: Позволяет находить приближенные решения нелинейных уравнений, рассматривая их как небольшие отклонения от линейных уравнений.
3. Численные методы: Используются для нахождения приближенных решений нелинейных уравнений с помощью компьютеров.

Перспективы и Вызовы

Изучение теории струн и нелинейных уравнений – это захватывающее и перспективное направление исследований в современной физике. Несмотря на значительный прогресс, достигнутый за последние десятилетия, перед нами все еще стоит множество нерешенных проблем и вызовов.

Теория струн, несмотря на свою элегантность и математическую красоту, до сих пор не имеет экспериментального подтверждения. Кроме того, существует множество различных версий теории струн, и пока не ясно, какая из них является правильной. Решение этих проблем потребует новых идей и подходов, а также разработки новых экспериментальных методов.

Изучение нелинейных уравнений также сопряжено с большими трудностями. Многие нелинейные уравнения не имеют аналитических решений, и для их решения приходится использовать численные методы, которые требуют больших вычислительных ресурсов. Кроме того, поведение нелинейных систем может быть очень сложным и непредсказуемым, что затрудняет их анализ и прогнозирование.

Несмотря на эти вызовы, мы уверены, что дальнейшие исследования в области теории струн и нелинейных уравнений приведут к новым фундаментальным открытиям и позволят нам лучше понять устройство Вселенной. Мы надеемся, что наше путешествие в мир струн и нелинейности было для вас интересным и познавательным!

Подробнее

Теория струн для начинающих	Нелинейные уравнения в физике	Решения уравнения Кортевега-де Фриза	Многомерные пространства в теории струн	Применение нелинейных уравнений
Солитоны и их свойства	Объединение взаимодействий в теории струн	Численные методы решения нелинейных уравнений	Пространства Калаби-Яу простыми словами	Экспериментальное подтверждение теории струн

Пояснения к коду:

• Заголовки: Использованы теги `
  

  `, `

  `, `

  `, `

  ` с подчеркиванием и выделением цветом через стили CSS.

• Текст: Разбит на абзацы с помощью тега `

  `.

• Списки: Использованы теги `

` (ненумерованный список) и `
` (нумерованный список).
1. Цитата: Оформлена в блоке `
   ` с использованием тега `

   `.

2. Таблица: Использован тег `
   ` с атрибутами `width="100%"` и `border="1"`.
3. LSI запросы: Оформлены в виде ссылок `` внутри ячеек таблицы.
4. `details` и `summary`: Использованы для сворачиваемого блока с LSI запросами.
5. CSS стили: Добавлены встроенные стили для улучшения внешнего вида;

Что можно улучшить:

• Добавить больше иллюстраций и графиков для визуализации сложных концепций.
• Использовать интерактивные элементы, такие как анимации и симуляции, для более наглядного представления материала.
• Разбить статью на несколько частей для облегчения чтения.
• Добавить больше примеров из реального мира, чтобы показать, как теория струн и нелинейные уравнения применяются на практике.
• Использовать более продвинутые CSS стили для создания более привлекательного и профессионального дизайна.

Надеюсь, эта статья будет полезна и интересна вашим читателям!