Теория струн: Танец математики и физики в некоммутативном пространстве

Приветствую вас, дорогие читатели! Сегодня мы с вами отправимся в захватывающее путешествие в мир теоретической физики, где математика и физика переплетаются в удивительном танце. Мы поговорим о теории струн и ее связи с некоммутативной геометрией – областях, которые кажутся далекими от повседневной жизни, но на самом деле пытаются ответить на самые фундаментальные вопросы о природе Вселенной.

Мы, как любознательные исследователи, всегда стремимся понять, как устроен мир вокруг нас. От мельчайших частиц до огромных галактик – все подчиняется определенным законам. Но что, если эти законы не такие простые, как нам кажется? Что, если пространство и время, которые мы привыкли считать гладкими и непрерывными, на самом деле имеют более сложную структуру?

Теория струн – это попытка объединить все известные силы природы в единую теорию. Вместо того чтобы рассматривать элементарные частицы как точечные объекты, теория струн предполагает, что они являются крошечными вибрирующими струнами. Различные моды колебаний этих струн соответствуют различным частицам, таким как электроны, кварки и фотоны.

Представьте себе гитарную струну. В зависимости от того, как вы ее дергаете, она издает разные звуки. Точно так же, в теории струн, различные способы вибрации струн соответствуют разным типам частиц. Это элегантное и красивое объяснение того, почему существует так много различных частиц в природе.

Проблемы Стандартной модели

Стандартная модель – это текущая лучшая теория, описывающая известные элементарные частицы и силы, за исключением гравитации. Она успешно объясняет многие явления, но имеет и недостатки:

• Не включает гравитацию.
• Требует большого количества параметров, которые необходимо измерять экспериментально.
• Не объясняет темную материю и темную энергию.

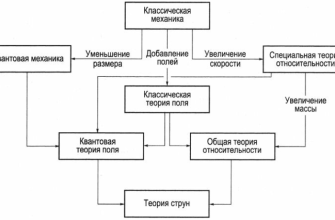
Теория струн обещает решить эти проблемы, объединив гравитацию с другими силами и предложив более фундаментальное описание Вселенной.

Некоммутативная геометрия: Искривление пространства

Некоммутативная геометрия – это раздел математики, который изучает пространства, где обычные правила геометрии не работают. В обычной геометрии порядок, в котором мы выполняем операции, не имеет значения. Например, поворот на 90 градусов по часовой стрелке, а затем сдвиг на 10 метров дает тот же результат, что и сдвиг на 10 метров, а затем поворот на 90 градусов.

Однако в некоммутативной геометрии порядок операций имеет значение. Это означает, что пространство может быть "искривлено" таким образом, что привычные нам представления о расстоянии и направлении становятся размытыми.

Алгебра и геометрия

Одной из ключевых идей некоммутативной геометрии является то, что геометрию можно описать алгебраически. Вместо того чтобы изучать точки и линии, мы изучаем алгебры функций на этих пространствах. В обычной геометрии эти алгебры являются коммутативными, то есть порядок умножения функций не имеет значения. Однако в некоммутативной геометрии эти алгебры могут быть некоммутативными, что приводит к новым и интересным геометрическим структурам.

Представьте себе, что вы пытаетесь определить местоположение объекта, используя два разных способа измерения. В обычной геометрии вы получите один и тот же результат, независимо от того, какой способ измерения вы используете первым. Но в некоммутативной геометрии результаты могут отличаться, что указывает на то, что пространство "искривлено" или "некоммутативно".

Связь между теорией струн и некоммутативной геометрией

Итак, как же связаны теория струн и некоммутативная геометрия? Оказывается, что теория струн часто приводит к появлению некоммутативных пространств. Например, при изучении струн в присутствии фонового магнитного поля, эффективная геометрия, которую "видят" струны, становится некоммутативной.

Это означает, что на очень малых масштабах, сравнимых с размером струны, пространство может быть не таким гладким и непрерывным, как мы привыкли думать. Вместо этого оно может иметь дискретную или "квантованную" структуру, которая описывается некоммутативной геометрией.

Матричная теория

Одним из конкретных примеров связи между теорией струн и некоммутативной геометрией является матричная теория. Матричная теория – это формулировка теории струн, в которой пространство-время описывается матрицами, а не числами. Матрицы не коммутируют, то есть порядок умножения матриц имеет значение. Это приводит к некоммутативной геометрии пространства-времени.

Представьте себе, что вы пытаетесь описать положение объекта в пространстве, используя матрицы. В обычной геометрии вы бы использовали числа для обозначения координат объекта. Но в матричной теории вы используете матрицы. Поскольку матрицы не коммутируют, порядок, в котором вы умножаете матрицы, имеет значение, что приводит к некоммутативной геометрии.

Приложения

Связь между теорией струн и некоммутативной геометрией имеет множество потенциальных приложений. Она может помочь нам понять природу пространства-времени на самых малых масштабах, а также разработать новые теории гравитации и космологии.

Например, некоммутативная геометрия может помочь нам понять, что происходит внутри черных дыр, где гравитация настолько сильна, что обычные законы физики перестают работать. Она также может помочь нам понять природу темной материи и темной энергии, которые составляют большую часть массы и энергии Вселенной.

Теория струн и некоммутативная геометрия – это сложные и увлекательные области исследований, которые пытаются ответить на самые фундаментальные вопросы о природе Вселенной. Они предлагают нам новый взгляд на пространство-время и гравитацию, а также могут привести к новым открытиям в физике и математике.

Мы надеемся, что это путешествие в мир теории струн и некоммутативной геометрии было для вас познавательным и интересным. Мы продолжим следить за развитием этих областей и делиться с вами новыми открытиями и идеями.

Спасибо за внимание!

Подробнее

Квантовая гравитация	Экстра измерения	Калибровочные теории	Компактификация	Дуальности в теории струн
Матричная модель	Некоммутативное пространство-время	Теория суперструн	Геометризация физики	Квантовая теория поля